Circulatory system and blood v

[laczlacylaci]

I'm listing the whole mechanism & blood v comparison of the circulatory system, feel free to correct if I am wrong.
Oxygenated blood=OB
Deoxygenated blood=DOB
1) OB flows from LUNG ->relaxed LA through Pulmonary Vein
2) LA contracts->OB blood flows to relaxed LV through Mitral Valve
3) LV contracts-> OB blood goes through aorta valve to periphery through arteries
4) arteries get branched into capillaries (OB->DOB) Oxygen diffuses to necessary organs
5) Capillaries become Veins carrying DOB
6) as RA relaxes, DOB flows in through Vena Cava
7) RA contracts; RV relaxes, DOB flows into RV through tricuspid valve
8) RV contracts and pushed DOB to pulmonary artery through pulmonic valve
9) DOB goes to lung from pulmonary artery->capillaries (exchange gases) and repeats the circulatory system.

According to the continuous equation, as A increases, v decreases.
So comparing blood v:
arteries=veins<arterioles=venule<capillaries?
This is because we compare TOTAL cross-sectional area. Correct?

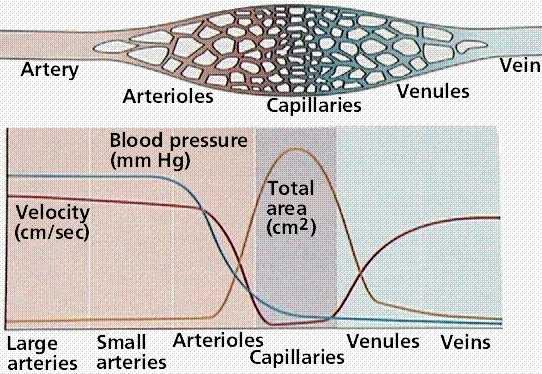
So here, we can see that A and v are inversely proportional due to the continuous equation (A1v1=A2v2)
As for BP, why are veins lower than arteries? Does this have to do with P1V1=P2V2? But I don't know if there is a difference in volume between the 2...

---

Members don't see this ad.

 

[theonlytycrane]

The capillaries have the largest total area, so they have the smallest velocity. This makes sense because nutrients are absorbed in the tissues at the thin capillary vessels and we don't want those nutrients speeding by before they can be taken up.

The circulatory system flow looks good. For the heart, I remember that the tri-cuspid valve comes before the bi-cuspid valve going from the right side to the left because you always "tri" before you "bi".

I also always pair the continuity equation with bernoulli's equation (conservation of energy for fluids).

a1v1 = a2v2 and fluid-density * g * h + Pressure + 1/2 * fluid-density * v^2 = constant.

A common question always goes like this: Vessel A has more area than Vessel B. How does the pressure of Vessel A compare to B?

Use the continuity equation to see that Vessel A has a larger area and lower velocity. Then use bernoulli's equation to see that Vessel A has a lower velocity, so it has a higher pressure.

 

[laczlacylaci]

The capillaries have the largest total area, so they have the smallest velocity. This makes sense because nutrients are absorbed in the tissues at the thin capillary vessels and we don't want those nutrients speeding by before they can be taken up.

The circulatory system flow looks good. For the heart, I remember that the tri-cuspid valve comes before the bi-cuspid valve going from the right side to the left because you always "tri" before you "bi".

I also always pair the continuity equation with bernoulli's equation (conservation of energy for fluids).

a1v1 = a2v2 and fluid-density * g * h + Pressure + 1/2 * fluid-density * v^2 = constant.

A common question always goes like this: Vessel A has more area than Vessel B. How does the pressure of Vessel A compare to B?

Use the continuity equation to see that Vessel A has a larger area and lower velocity. Then use bernoulli's equation to see that Vessel A has a lower velocity, so it has a higher pressure.

But would that apply to let's say capillaries vs. arteries?
capillaries A>arteries A, so I would assume the pressure if higher in caps than arteries... which wouldn't make sense...
Or is the vessel idea, only comparing one vessel cross-sectional area, not the total?

 

[theonlytycrane]

Yeah- just a rough approximation between the cross-sections of two vessels.

Capillaries vs. arteries gets more complicated because it can depend on which capillary / artery we're talking about and bernoulli's equation also has the density * g * h term which includes height. The simplified vessel example assumed everything was constant except for area.

 

[laczlacylaci]

A common question always goes like this: Vessel A has more area than Vessel B. How does the pressure of Vessel A compare to B?

Use the continuity equation to see that Vessel A has a larger area and lower velocity. Then use bernoulli's equation to see that Vessel A has a lower velocity, so it has a higher pressure.

Essentially, this is large area->low v->high pressure so can we assume with larger area, we will have larger pressure?

In this question, the passage states that NO gas relaxes smooth muscles. Bringing that to the circulatory system, it would expand/vasodilate arteries=increases area, why would it not increase blood pressure in this case?

Instead, would it makes sense that I assume:
increase in Area=lower v=decrease in pressure=increase in volume?

But that would totally change vessel A in having increased area, lower velocity, lower pressure, higher volume than vessel B...

 

[laczlacylaci]

This is little confusing since
Bernoulli eq: as we increase velocity, pressure decreases
Boyle's law: as we increase volume, pressure decreases
Continuous eq: as we decreases area, velocity increases

Can I assume: decreases area=velocity increases=decrease in pressure=increase in volume?

But then that wouldn't match the question I posted... 🙁

 

[theonlytycrane]

The continuity equation / Bernoulli's equation allows for rough approximations when comparing between two vessels where most things are held constant.

In the problem posted, focus more on whether the vessel is vasodilating or vasoconstricting and remember that dilation -> decreases b.p. and constriction -> increases b.p.

Getting the above 2 equations and situation to all line up is hard because there's a lot of variables and we're approximating a lot anyway. For example, no two vessels will be at exactly the same height. This is kind of an unsatisfying explanation, but go with 2 different approaches based on whether you're comparing vessels or thinking about constriction / dilation.