D
deleted647690
There was a question in uworld that presented a picture of a polyprotic acid titration curve. It showed the titration of H3PO4 by NaOH. According to this curve:
At the first equivalence point: [H2PO4 -] = [OH-]
At the second equivalence point: [HPO4 2-] = 1/2 [OH-]
At the third equivalence point: [PO4 3-] = 1/3[OH-]
I'm having trouble understand how they came up with these ratios. I know that, at the half equivalence point, the concentration of an acidic species in solution is = the concentration of its conjugate base.
Also, at an equivalence point, one equivalent of OH- has been added to fully neutralize the acidic species.
Therefore, I'd expect these ratios:
1st equivalence point: [H3po4] = [OH-]
2nd equivalence point: [H2PO4-] = [OH-], and therefore, [H3PO4] = 2*[OH-]
3rd equivalence point: [HPO42-] = [OH-], and therefore, [H3PO4] = 3*[OH-].
Here is a picture of a titration curve for H3PO4 for reference:
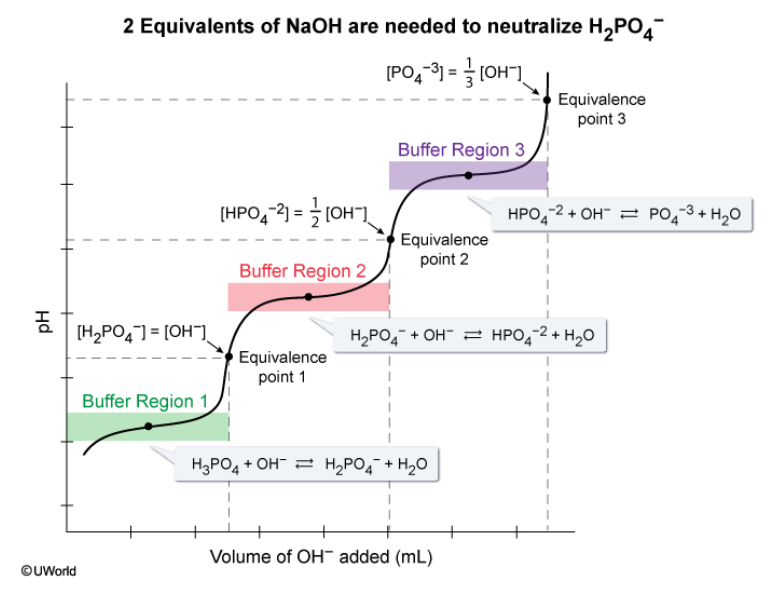
At the first equivalence point: [H2PO4 -] = [OH-]
At the second equivalence point: [HPO4 2-] = 1/2 [OH-]
At the third equivalence point: [PO4 3-] = 1/3[OH-]
I'm having trouble understand how they came up with these ratios. I know that, at the half equivalence point, the concentration of an acidic species in solution is = the concentration of its conjugate base.
Also, at an equivalence point, one equivalent of OH- has been added to fully neutralize the acidic species.
Therefore, I'd expect these ratios:
1st equivalence point: [H3po4] = [OH-]
2nd equivalence point: [H2PO4-] = [OH-], and therefore, [H3PO4] = 2*[OH-]
3rd equivalence point: [HPO42-] = [OH-], and therefore, [H3PO4] = 3*[OH-].
Here is a picture of a titration curve for H3PO4 for reference:
