Question about fluid density

[rinsterman12]

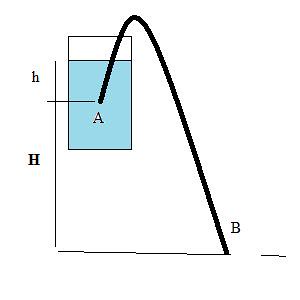
The question is about a fish tank. If one were filled with water and the other was filled with something more dense than water. How would the velocity at a point at the end of a siphon which is placed into the tank at one end.
The answers are as followed:
A) less than the velocity of water because a greater force would be required to accelerate the greater mass
B) equal velocity of water
C) greather than the velocity of water b/c greater pressure is created by higher density fluid
D) Greather than velocity of water b/c greater mass has more potential to convert to kinetic

How is the velocity the same. The answers says the acceleration of the two fluids the same and the velocity. Would anyone explain this to me. This is under ideal conditions.

---

Members don't see this ad.

 

[DrSmday]

using Bernoulli's equation velocity of a fluid at an opening is equal to the square root of 2gh where g is the acceleration due to gravity and h is the height of the opening.... from that equation you can see that the velocity does not depend on the density of the fluid...

hope that helps

 

[Vanguard23]

using Bernoulli's equation velocity of a fluid at an opening is equal to the square root of 2gh where g is the acceleration due to gravity and h is the height of the opening.... from that equation you can see that the velocity does not depend on the density of the fluid...

hope that helps

Viscocity is factored into flow rate via velocity of the fluid; viscocity and density being pretty directly proportional.
Viscous ******ing force:
F= 4*pi*eta(viscocity)*L*v
Greater viscocity = lower velocity = lower flow rate

I think the answer lies in a cancellation. The pressure from the denser fluid is greater(rho*g*h), however, a denser fluid has a lower velocity. So, greater velocity from the greater pressure, but lower velocity from a higher viscocity.

 

[TFS]

flow rate is equal to area x velocity

poiseuille's law tells you that flow rate has no dependence on density, only viscosity, radius of the tube, length, and the pressure difference.

therefore, density has no effect on velocity. since all the other variable in poiseuille's equation stay the same, flow rate will be unchanged, and since area is unchanged as well, velocity will not change.

 

[RogueUnicorn]

Viscocity is factored into flow rate via velocity of the fluid; viscocity and density being pretty directly proportional.
Viscous ******ing force:
F= 4*pi*eta(viscocity)*L*v
Greater viscocity = lower velocity = lower flow rate

I think the answer lies in a cancellation. The pressure from the denser fluid is greater(rho*g*h), however, a denser fluid has a lower velocity. So, greater velocity from the greater pressure, but lower velocity from a higher viscocity.

this is untrue

 

[Vanguard23]

this is untrue

Well which part?

 

[kentavr]

In the tank at point of tube opening:
E=P + rgh + rv^2/2, Where P = rgH (H-hight of tank) and v=0 =>
E=rgH+rgh

At the bottom of thetube
E=P+rgh+rmv^2/2 (P=0,h=0) => E=rv^2/2

By bernoulli,
rgh+rgH = rv^2/2

r is gone, since it is on the left and right. the final speed does not depend on density(r).

 

[kokocipher]

Were the tanks in the same level of height or different? I think the problem only said that one tank was filled with something more dense than water. If this is true, then you cannot have

"At the bottom of thetube
E=P+rgh+rmv^2/2 (P=0,h=0) => E=rv^2/2"


If
P1+r1gh+1/2(r1)(v1^2) = P2+r2gh+1/2(r2)(v2^2)

and that r1 < r2, then logically, the liquid with r2 should have a lower v. The only way the two v are equal is if P2 is lower than P1. P is the pressure at the surface of the fl., so it's just atm. pressure, thus both P1 and P2 should be the same.

I'm a bit confused by the problem as well, can you type exactly what the problem says? If there was a diagram, can you please upload an image?

 

[kentavr]

Were the tanks in the same level of height or different? I think the problem only said that one tank was filled with something more dense than water.

I would assume that both tanks have the same elevation H, otherwise, even the answer for the same liquid will be different.

If this is true, then you cannot have
"At the bottom of thetube
E=P+rgh+rmv^2/2 (P=0,h=0) => E=rv^2/2"

This exactly what I should have if the tube is open to atmosphere (P=1 atm). The atmospheric pressure can be nullify from both side of equation.

If
P1+r1gh+1/2(r1)(v1^2) = P2+r2gh+1/2(r2)(v2^2)

This is wrong.
It is true that:
P1+r1gh+1/2(r1)(v1^2)=const
and
P2+r2gh+1/2(r2)(v2^2)=const
but this constants are different for two different liquids.

I'm a bit confused by the problem as well, can you type exactly what the problem says? If there was a diagram, can you please upload an image?

Let's see if the author will clarify. But I would expect something like this

At point A: E=rgH + rgh
At point B: E=rv^2/2
then divide by r(rho) both sides and it shows that speed at point B is not dependent on density. Strange, not obvious, but seems like so.