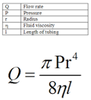Change in Blood Vessel radius

[taylorswift132]

Can someone please help me with this question? (Using Poiseuille's Law)

Suppose a blood vessel's radius is decreased to 90.0% of its original value by plaque deposits and the body compensates by increasing the pressure difference along the vessel to keep the flow rate constant. By what factor must the pressure difference increase?

Thanks!

---

Members don't see this ad.

 

[Neuroplasticity]

To keep Q constant, if r is now 0.9 of what it was before, P must be changed by 1/(0.9^4) = 1.5

With algebra, to keep the same flow rate:
Q = [(pi)*(P1)*(r1)^4] / [8nl]
Q = [(pi)*(P2)*(r2)^4] / [8nl]
So Q = [(pi)*(P1)*(r1)^4] / [8nl] = [(pi)*(P2)*(r2)^4] / [8nl]
Simplifying, P1*r1^4 = P2*r2^4
(r2/r1)^4 = P1/P2 and r2/r1 = 0.9
P1 = 0.9^4 * P2
P2 = P1 / (0.9^4)
So the new pressure drop required is ~1.5 times original pressure difference