index of refraction & critical angle

[arc5005]

Passage:

If this experiment were carried out in water instead of air, what would be expected?


A. the critical angle would be smaller in water than air; the angle of refraction would be greater in water than air.
B. the critical angle would be smaller in water than air; the angle of refraction would be smaller in water than air.
C. the critical angle would be greater in water than air; the angle of refraction would be greater in water than air.
D. the critical angle would be greater in water than air; the angle of refraction would be smaller in water than air.

D) the critical angle would be greater in water than air; the angle of refraction would be smaller in water than air.

The index of refraction for water is greater than the index of refraction for air, so light passing from the disk to water will be bent less than light passing from the disk to air. This means that the angle of refraction is smaller in water than air, eliminating A and C. In order to get a refracted angle of 90° in water, a greater incident angle is required than what is required to get a refracted angle of 90° in air. Thus, the critical angle between the disk and air is less than it is between the disk and water. D is the best answer.

----------

I'm trying to picture this:

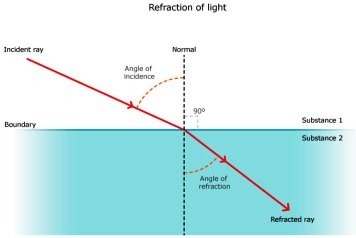
so, when water the light goes from DISK -> AIR there is a greater index of refraction for air, because air has a smaller index of refraction. Basically...

if n1 = air, n2 = disk, n3 = water:

n1 * sin theta1 = n2 * sin theta2

Disk -> Air:
sin theta1 = (n2/n1) * sin theta 2

Disk -> water:
sin theta3 = (n2/n3) * sin theta 2

because, n3 > n2, then sin theta3 < sin theta1, so the angle of refraction of air > water. This means that the angle of refraction is smaller in water than air, eliminating A and C.

------

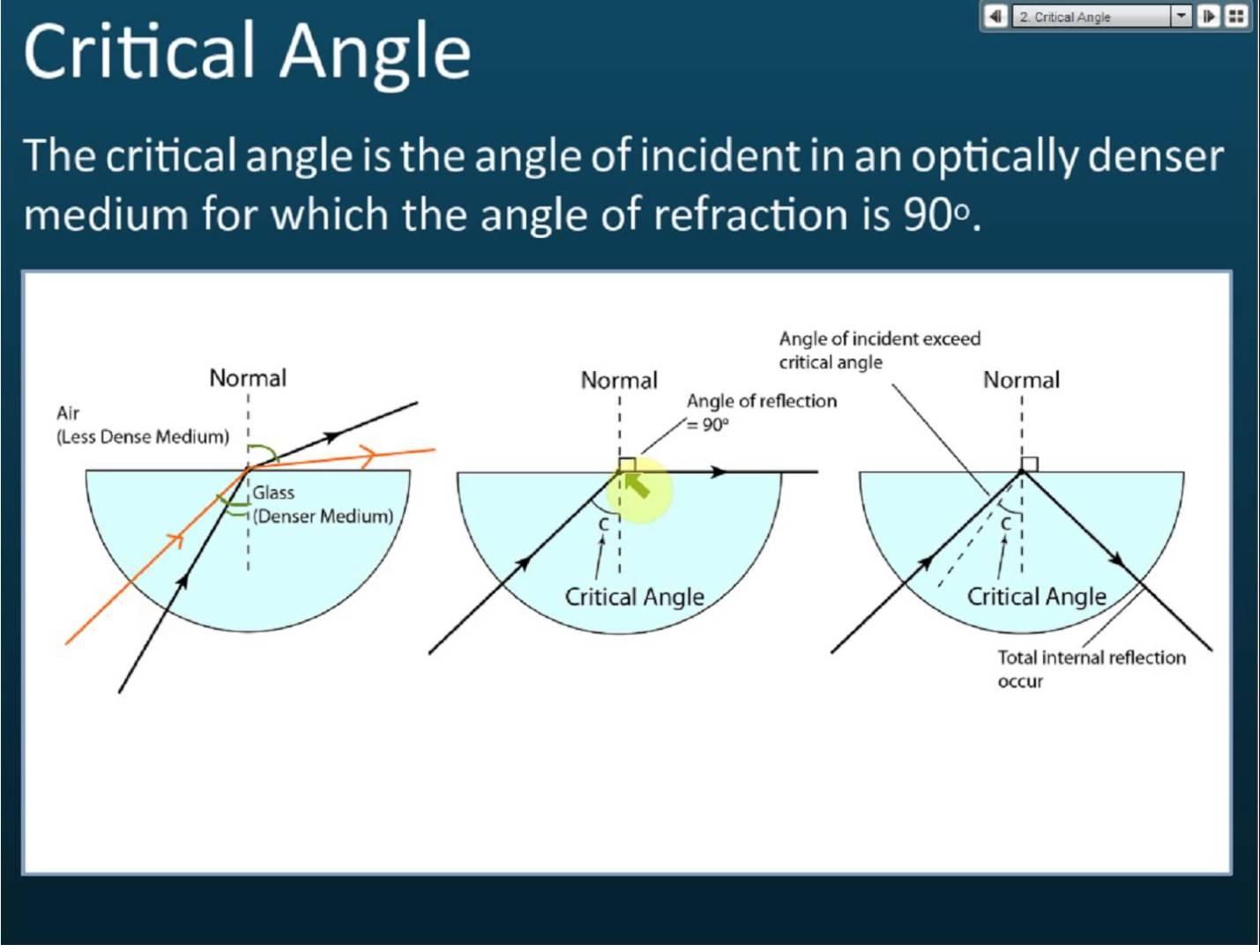
Then next... is the part I'm having difficulty with Critical Angle:

"In order to get a refracted angle of 90° in water, a greater incident angle is required than what is required to get a refracted angle of 90° in air. Thus, the critical angle between the disk and air is less than it is between the disk and water. D is the best answer." ??

Basically, what they are trying to say is that: the disk is a denser medium than air or water, so when you go from a denser medium -> a lighter medium you can can have a total internal reflection occur which is when the angle of incident is larger than the critical angle. The critical angle is the angle when the angle of refraction is 90 degrees, so... I would assume you would use snell's law again:

Disk -> Air
(n_material) * (sin theta_critical) = (n_air) * (sin theta_air)
(n_material) * (sin theta_critical) = (n_air) * (sin 90)
(sin theta_critical) = (n_air) * (sin 90) / (n_material)

Disk -> Water:
(n_material) * (sin theta_critical) = (n_w) * (sin theta_w)
(n_material) * (sin theta_critical) = (n_w) * (sin 90)
(sin theta_critical) = (n_w) * (sin 90) / (n_material)

So because n_w > n_air, then you get a larger critical angle for water than a critical angle for air?

---

Members don't see this ad.

 

[hebrewBAMmer]

If the two mediums are the same, the light would pass in a straight line. The difference in mediums causes the light ray to bend. So if you have water instead of air, the difference between the index of refraction of the two mediums is less than the difference than it is with air, so the line is closer to straight, and hence the angle of refraction is less (that eliminated A and C)

For the same reason, the critical angle is larger because in your bottom figure, now your black line is "more straight", so you can turn it more before it completely reflects internally. That leaves you with D

 

[arc5005]

If the two mediums are the same, the light would pass in a straight line. The difference in mediums causes the light ray to bend. So if you have water instead of air, the difference between the index of refraction of the two mediums is less than the difference than it is with air, so the line is closer to straight, and hence the angle of refraction is less (that eliminated A and C)

For the same reason, the critical angle is larger because in your bottom figure, now your black line is "more straight", so you can turn it more before it completely reflects internally. That leaves you with D

thanks! that helps.