The question asks for the total number of possible stereoisomers. (question below)
Normally when you have a stereocenter that is attached to a ring you still count the 2 stereoisomers that arise from that stereocenter. Why is it different in this case?
The explanation says (shown below) that because of the cyclic nature of the molecule, not all stereocenters can be inverted.
But then why is are there 2 possibilities then? If you cant switch anything around, wouldn't it just be 1 stereoisomer?
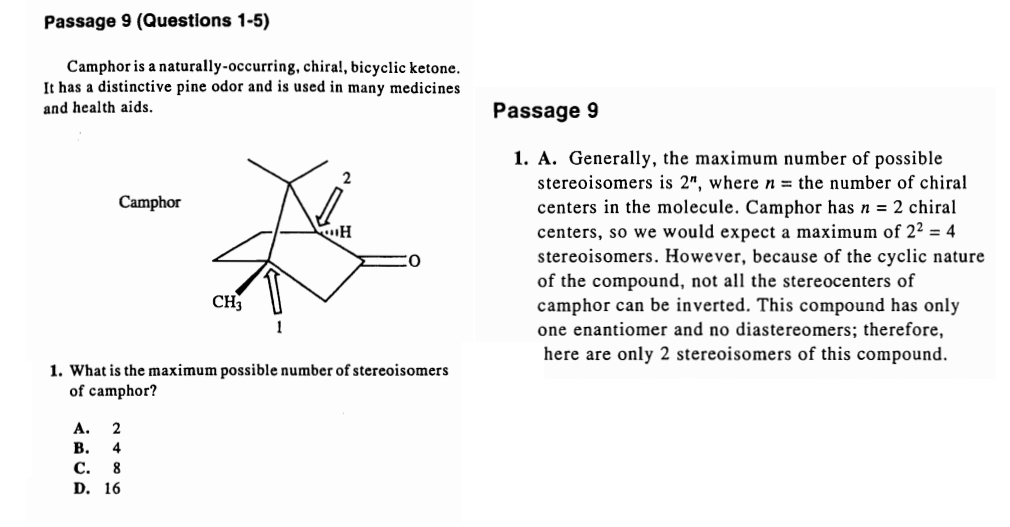
Normally when you have a stereocenter that is attached to a ring you still count the 2 stereoisomers that arise from that stereocenter. Why is it different in this case?
The explanation says (shown below) that because of the cyclic nature of the molecule, not all stereocenters can be inverted.
But then why is are there 2 possibilities then? If you cant switch anything around, wouldn't it just be 1 stereoisomer?

