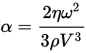Sound Attenuation

[MedPR]

From mcat-review:

• Sound attenuation is the gradual loss of intensity as sound travels through a medium.
• Sound attenuation is the greatest for soft, elastic, viscous, less dense material.

I don't follow this at all. Based only on the fact that it says soft sound has the greatest attenuation, I'm assuming "greatest attenuation" means "becomes inaudible in the least amount of time." Is that right?

If yes, then I'm not sure I understand why sound attenuation is greatest in elastic, viscous, and less dense material.

I understand that sound travels faster in a more elastic material and less dense material, but doesn't sound travel more slowly in viscous material? So it makes sense to me that the faster the sound wave travels, the quicker it attenuates and becomes inaudible, but if viscous media slows down sound waves, wouldn't it make the sound take longer to attenuate?

---

Members don't see this ad.

 

[chiddler]

Attenuation just means weakening, or losing intensity. An attenuated virus in vaccination is a virus that is less effective than the normal strain.

Look at it from an energetic point of view. If the medium is viscous, then a moving sound wave will have to produce longitudinal waves in material that has strong intermolecular bonds. Not very easy and energy will dissipate quickly. Same story for a dense material: the sound wave has to move a lot of weight in order to propagate and is thus dissipated quickly.

I am not sure about the molecular reason for elasticity. I am also not sure if you can relate velocity and attenuation directly. Can you? I don't think so because a slower wave does not mean a weaker wave.

 

[MedPR]

Attenuation just means weakening, or losing intensity. An attenuated virus in vaccination is a virus that is less effective than the normal strain.

Look at it from an energetic point of view. If the medium is viscous, then a moving sound wave will have to produce longitudinal waves in material that has strong intermolecular bonds. Not very easy and energy will dissipate quickly. Same story for a dense material: the sound wave has to move a lot of weight in order to propagate and is thus dissipated quickly.

I am not sure about the molecular reason for elasticity. I am also not sure if you can relate velocity and attenuation directly. Can you? I don't think so because a slower wave does not mean a weaker wave.

mcat-review says that a less dense material has greater attenuation, you are saying the opposite.

I'm not saying a slower wave means a weaker wave. I'm saying that a wave that moves faster probably loses energy faster because it is coming into contact with more particles and thus transfering energy more frequently. So it will lose all its energy and thus be inaudible faster. Maybe that's not right though?

 

[chiddler]

mcat-review says that a less dense material has greater attenuation, you are saying the opposite.

I'm not saying a slower wave means a weaker wave. I'm saying that a wave that moves faster probably loses energy faster because it is coming into contact with more particles and thus transfering energy more frequently. So it will lose all its energy and thus be inaudible faster. Maybe that's not right though?

No i'm agreeing. More dense means that the wave will have to move more mass and therefore will weaken faster.

I've no idea about the rate of energy loss, though. My first thought is what if it's a faster wave in X, but a more efficient (loses less energy) in Y, although slower.

 

[MedPR]

No i'm agreeing. More dense means that the wave will have to move more mass and therefore will weaken faster.

I've no idea about the rate of energy loss, though. My first thought is what if it's a faster wave in X, but a more efficient (loses less energy) in Y, although slower.

Yea, more dense means weakens faster, which means greater attenuation, right?

mcat-review says less dense = greater attenuation.

 

[chiddler]

oh, whoops.

i'll post on physicsforums later; maybe we'll get more help there.

 

[MedChad]

So I am reading this thread and see that medpr says " that sound travels faster in less dense material", which I believe makes sense. But TBR says the opposite on page 6 of Physics 2 and says "the general trend for speed of sound is v in solid > v in liquid > v in gas. Later it states density of solid is generally greater than liquid or gas. So whats right? Sorry for getting off the topic, I just had to ask.

 

[chiddler]

it means if you compare similar material (solid vs solid) and compare their densities, then the one with less density wins.

comparing different phased materials, you have to account for both bulk modulus and density.

That said, bulk modulus for a gas is very low, and density is even lower. So...you have more things to consider and is not as simple a comparison.

 

[milski]

There is a formula for attenuation in fluids which takes into account the density. I think that's beyond what MCAT tests but it is correct that higher density has lower attenuation (less losses in high density materials).

The losses are not related at all to the mass of whatever you're moving, you just move them less. The losses come from not being able to transmit all of the energy to the next particle as the wave propagates. That's more pronounced in less dense fluids where the particle is further away from its neighbor and it's 'harder' to transfer that energy without losses.

I'm not sure how speed of sound got involved but in general things are much more complicated there. In fluids (not gasses), it will depend on the density of the fluid. In gasses, it won't. Again, I don't know how much detail is expect for the MCAT on this subject.

 

[Saigon]

I know this is a super old question but I was confused by the same thing on mcat-review.org. After some struggling I think I figured out the answer.

So, "Sound attenuation is the greatest for soft, elastic, viscous, less dense material." We will define attenuation as a reduction in signal.

Stoke's law of sound attentuation ->

, where n = viscosity, w = frequency, p = density, and V = velocity.

viscosity - it makes sense that there would be more attenuation as viscosity increases. viscosity defined as the extent to which a fluid resists a tendency to flow. a more viscous fluid has greater friction and does more work against the propagating sound wave. we know that a wave is a transport of energy, so work done against it means there is less energy being propagated.

frequency - the number of wave oscillations per second. the more oscillations the more compressions of the air particles. more compressions means more energy lost as heat = greater signal attenuation

density - the less dense the medium the greater distance between air particles and the less chance propagation = reduced signal. energy has a greater chance of being absorbed into matter.

velocity - speed of a longitudinal wave:

first, you need to remember the definitions of bulk and young's moduli. a bulk modulus describes a material's compressibility. the speed of sound in a liquid is greater than a speed of sound in a gas because the bulk modulus in liquids is GREATER. the bulk modulus is used to describe the inverse of a substance's compressibility. since liquids are less compressible than solids their bulk modulus is greater so sounds propagate through them faster.

young's modulus is the ratio of stress/strain. basically it describes how much a material deforms when you apply a certain force to it. steel has a greater young's modulus than rubber because you can apply a lot of force to try and bend steel but nothing will happen, while if you apply a lot of force to deform a rubber band that's easy.

so in order to maximize attenuation we want to minimize velocity, which would decrease the denominator in Stoke's law. to decrease velocity we want to decrease the bulk/young's modulus, hence we want to use soft and elastic materials. elastic materials are those with a lower young's modulus which decreases the numerator in the velocity equation, which decreases velocity and increases sound attenuation. soft could refer to the bulk moduli. something softer is more compressible which means it has a smaller bulk modulus, which decreases velocity and increases sound intensity.

caveat: there is a caveat, which is the density term in the speed of a longitudinal wave equation. if you only considered this equation then you would think that we want to use more dense objects to decrease velocity, and therefore increase sound attenuation. however, there are two things to note. as previously mentioned, sound travels faster in solids/liquids than gases even though they are both more dense than liquids. the increase in velocity due to the greater young/bulk moduli OUTWEIGHS the decrease in velocity due to the greater densities. similarly, if we were to substitute the longitudinal wave equation into Stoke's equation we would get the square root of the bulk/young moduli in the denominator and the square root of the density in the numerator. therefore, decreasing density in the denominator has a greater effect in increasing sound attenuation than the effect increasing density has on increasing sound attenuation. combining the equations also shows how we maximize attenuation by minimizing the bulk/young modulus = using more elastic/softer materials.

with regards to why a slower moving wave has greater attenuation I think it's probably due to the greater ability of the medium (matter) to absorb energy being transmitted.

I could be completely wrong about all this but it was really bugging me so I had to form some sort of a solution. I'm going to start answering every question I see on here. I should probably learn to shorten my answers :O