- Joined
- May 27, 2012
- Messages
- 2,107
- Reaction score
- 4,669
- Points
- 6,766
- Podiatrist
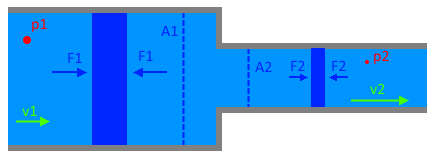
So This is what I understand.
When radius decreases, pressure increases. Due to P = F/A and area decreases.
When pressure increases, velocity decreases? I am confused as to why.
Is it due to the fact that resistance increases and this causes velocity to decrease?
But according to the continuity equation, AV= AV,
if
(10)x = 5(2), the initial velocity will be 1m/s while the pressure would be lower as well.
In this picture, why is the 1st region having a higher pressure? Shouldn't it have a lower pressure due to having a cross sectional area?

When radius decreases, pressure increases. Due to P = F/A and area decreases.
When pressure increases, velocity decreases? I am confused as to why.
Is it due to the fact that resistance increases and this causes velocity to decrease?
But according to the continuity equation, AV= AV,
if
(10)x = 5(2), the initial velocity will be 1m/s while the pressure would be lower as well.
In this picture, why is the 1st region having a higher pressure? Shouldn't it have a lower pressure due to having a cross sectional area?

Last edited: