- Joined
- Aug 13, 2006
- Messages
- 1,226
- Reaction score
- 14
Please refer to 61 in examkrackers physics textbook for helpful diagram
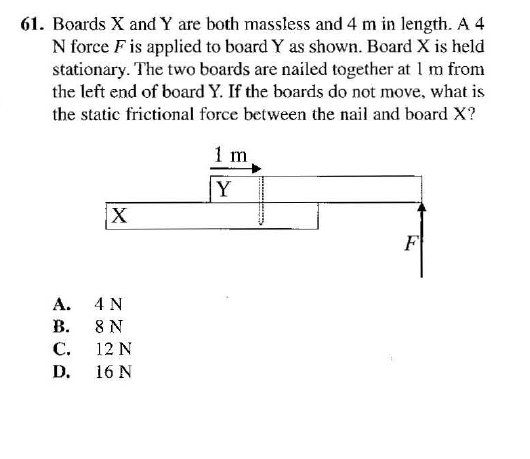
Boards X and Y are massless and 4m in length. A 4N force F is applied to board Y as shown. Board X is held stationary. The two boards are nailed together at 1m from the left end of board Y. If the boards do not move, what is the static frictional force between the nail and board X?
A. 4N
B. 8N
C. 12N
D. 16N
For this problem, I did not know where to begin at first. I choose the nail as the point of rotation. So 3m*4N=1m*F, which would equal F=12N which is C.
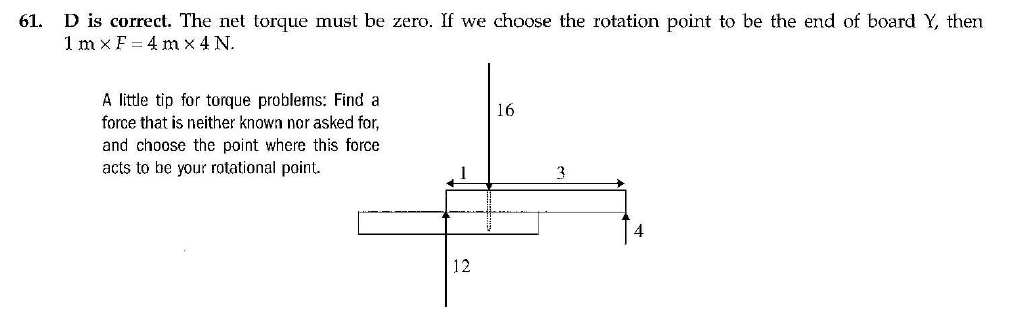
However, the answer is D. EK says The net torque must be zero. If we choose the rotation point to be the end of the board Y, then 1m*F=4m*4N and F=16N, D.
EK also includes a little hint A little tip for torque problems: Find a force that is neither known nor asked for, and choose the point where this force acts to be your rotational point.
I guess my two major problems with this question. I was not really clear what it was asking me. How do I know that is the static frictional force? And I seem to have a huge issue with choosing the point of rotation.
Can anyone help me and shed some light on these crazy torque problems.
Oh and one random further question Tension=mass*force of gravity, right?
Boards X and Y are massless and 4m in length. A 4N force F is applied to board Y as shown. Board X is held stationary. The two boards are nailed together at 1m from the left end of board Y. If the boards do not move, what is the static frictional force between the nail and board X?
A. 4N
B. 8N
C. 12N
D. 16N
For this problem, I did not know where to begin at first. I choose the nail as the point of rotation. So 3m*4N=1m*F, which would equal F=12N which is C.
However, the answer is D. EK says The net torque must be zero. If we choose the rotation point to be the end of the board Y, then 1m*F=4m*4N and F=16N, D.
EK also includes a little hint A little tip for torque problems: Find a force that is neither known nor asked for, and choose the point where this force acts to be your rotational point.
I guess my two major problems with this question. I was not really clear what it was asking me. How do I know that is the static frictional force? And I seem to have a huge issue with choosing the point of rotation.
Can anyone help me and shed some light on these crazy torque problems.
Oh and one random further question Tension=mass*force of gravity, right?