Analysis: LizzyM Scores for Any MCAT Scale

[Lawpy]

LAST EDIT: 11/8/2015

Spoiler: A New Metric for 2015 MCAT

The proposed new LizzyM-type score for the 2015 MCAT is:

Score = 10*(GPA + 2) + (MCAT - 500) (-8 <= score <= 88)

So I decided to do something fun here.

This analysis report will focus on the famous LizzyM score and its role with the new 2015 MCAT.

Classical LizzyM Score

This is defined as LizzyM = 10*GPA + MCAT, where the GPA is out of a 4.0 scale and the MCAT is out of a 45 scale. Since the new MCAT is based on an entirely different scale (ranging from 472 to 528), the ideal and accurate approach is to use the AAMC Percentile Conversion Tables prepared by @efle.

After about few cycles (typically Class of 2022 and thereafter), the conversion tables lose much of their value as the old MCAT becomes obsolete. What happens to the LizzyM score?

WedgeDawg's Linear Extension Model

Developed by @WedgeDawg in Aug 2015 in the Continued Validity of LizzyM Scores thread, the proposed conversion is Score = 10*(GPA - 1) + (MCAT - 500). The model is called linear, since we are dealing with just basic addition and subtraction. WedgeDawg redefined the scoring system from the usual 85-point scale, to a new 58-point scale.

You can see his post described here (and in the above link):

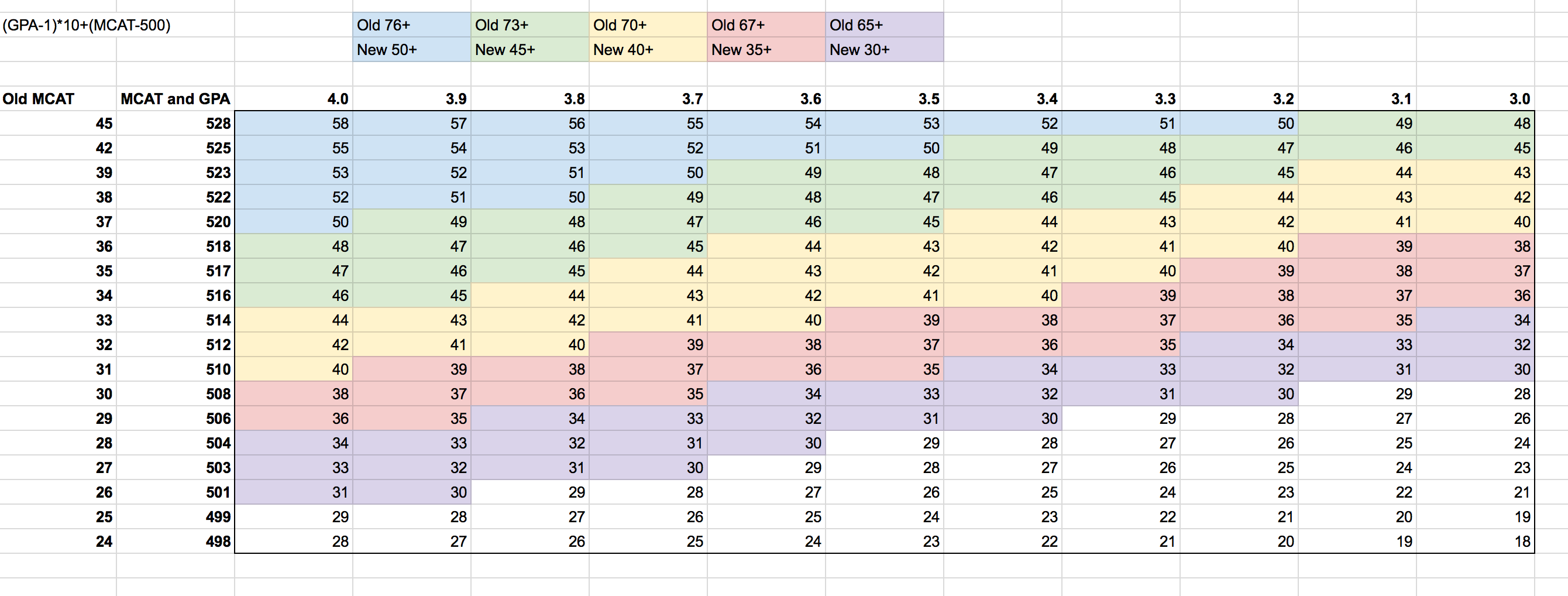
Alright guys, I have a proposed conversion for you all. The formula is:

(GPA-1)*10 + (MCAT-500) = Score

The max score (4.0/528) comes out to 58. I've gone through and made correlates between the old LizzyM score and the new one (which can be seen in the chart below). Examples:

Old 76 (i.e. 3.8/38 or 3.9/37) is new 50. This is generally the number to shoot for for top schools.

Old 73 (i.e. 3.8/35 or 3.9/34) is new 45. This is generally a good number for mid tiers while possibly being competitive for some top tiers.

Old 70 (i.e. 3.7/33 or 3.9/31) is new 40. This is generally where a "competitive" applicant for med school falls around.

Old 67 (i.e. 3.6/31 or 3.7/30) is new 35. This is around the accepted applicant median.

Old 65 (i.e. 3.6/29 or 3.7/28) is new 30. This is highly competitive for DOs and marginal for MD.

I didn't continue my color coordination after this, but you get the idea.

This score not only is easy to calculate, but provides convenient benchmarks for comparing scores to old LizzyM scores (down by 5's from 50 for new, down by 3's from 76 for old). It does break down at the MCAT extremes, but so did the old score (45/3.1 still gave you 76, for example).

Here are some spot checks:

3.7/32 is 69 old, which should be around 39ish new. Formula gives, for 3.7/512, 39, spot on!

3.4/38 is 72 old, which should be around 43-44 new. Formula gives, for 3.4/522, 46, so it's a little high, but it's also an extreme MCAT place.

3.9/32 is 71 old, which should be around 41-42 new. Formula gives, for 3.9/512, 41, right on!

3.3/36 is 69 old, which should be about 38-39 new. Formula gives, for 3.3/518, 41, so again, a little high.

This seems to work best the more "matched" the GPA and MCAT are, and gives slight favor to higher MCAT scores at the opposing extremes, but overall should be a decent estimate.

Obviously you can make it more accurate (by doing exact percentile conversions), but that would inevitably take away the simplicity of the calculation, which is the whole point. Also, because the new MCAT has multiple scores per old MCAT score, you're going to be hard pressed to find an algorithm that perfectly fits everything.

As we move away from old MCAT scores entirely, the conversion factor equality becomes far less important, and the balance between MCAT and GPA becomes the most important thing (here GPA is weighted out of 30 while MCAT is weighted out of 28, and the overall score can go as low as -32 if you have a 468 MCAT and 0.00 GPA). One MCAT point is still equivalent to 0.1 GPA points, just like the old scale.

See what you guys think!

Score-Mapping Model (via the Endpoint Method)

WedgeDawg's model is great and accurate, but it raises some questions and concerns. The most important involves changing the score range from 0 to 85 to -32 to 58, which seems difficult to switch and adjust after using the 0-85 scale for many years.

I propose an alternative, slightly more complicated model that addresses the above two concerns, while following the similar derivation approach to WedgeDawg's model. The model is generalized as:

Score = 10*GPA + (old MCAT range)/(new MCAT range) * (MCAT - lowest new MCAT score) (conversion formula)

This looks scary, so I will break it down:

new MCAT range = highest new MCAT score - lowest new MCAT score
old MCAT range = highest old MCAT score - lowest old MCAT score

The "new" and "old" terms are generalized and can be applied for any MCAT scale. For the 2015 MCAT, the model reduces to:

new MCAT range = 528 - 472 = 56
old MCAT range = 45 - 0 = 45

LizzyM = 10*GPA + (45/56) * (MCAT - 472) (LizzyM score for 2015 MCAT)

This model is also linear. The score becomes 0 for the lowest GPA and MCAT (0 and 472) and 85 for the highest GPA and MCAT (4 and 528), thus preserving the traditional LizzyM scoring range. Thus, the above model is MCAT-invariant. Likewise, the model prefers MCAT to GPA.

Equivalence of the Two Models and Complications

It's important to realize that WedgeDawg's model and the score-mapping model are really the same thing arranged differently. The equivalent relationship can be seen as follows:

Spoiler: Equivalence Calculations

LizzyM = 10*GPA + (45/56) * (MCAT - 472) ==>
LizzyM = 10*GPA + (45/56) * (MCAT - 500 + 28) ==>
LizzyM = 10*GPA + (45/56) * (MCAT - 500) + (45/56)*28 ==>
LizzyM = 10*GPA + (45/56) * (MCAT - 500) + 45/2 ==>
LizzyM = 10*GPA + 0.8 * (MCAT - 500) + 22.5 ==> (since no one likes fractions)
LizzyM = (10*GPA + 22.5) + 0.8 * (MCAT - 500) ==>
LizzyM = 10*(GPA + 2.25) + 0.8 * (MCAT - 500)

So we algebraically rearranged the model to resemble WedgeDawg's model.

Despite the rearrangement, the model remains complex. It is difficult to deal with fractions and decimals through mental computations, and the point of the LizzyM scores is to be done easily without using a calculator. Fortunately, the model can be reduced to simple terms.

Simple Metrics and Index Shifting

We can further simplify the model at the expense of slightly increasing the score range from 0 to 85 to -8 to 88. Doing so will provide the following simple and effective formula called the WedgeDawg-Lawper metric.

Score = 10*(GPA + 2) + (MCAT - 500) = 10*GPA + (MCAT - 480)

We can also readily derive the simple metric through a procedure called index shifting. Note that the classical LizzyM score is defined as:

LizzyM = 10*GPA + MCAT (0 <= LizzyM <= 85)

The good news is that the 10*GPA term is standardized per AMCAS rules, so it is unlikely to change. The MCAT term changes from 0 to 45 to 472 to 528. This is readily adjusted for by the following simple formula

Score = 10*GPA + (MCAT - 472) (0 <= score <= 96)

Note that this is similar to the classical LizzyM score written as 10*GPA + (MCAT - 0). The boundaries are found by setting GPA = 0, MCAT = 472 and GPA = 4, MCAT = 528.

Calculations for some rearrangements and index shifting are then:

Spoiler: Index Shifting Calculations

Score = 10*GPA + (MCAT - 472) (0 <= score <= 96) ==>
Score = 10*GPA + (MCAT - 500 + 28) (0<= score <= 96) ==>
Score = (10*GPA + 28) + (MCAT - 500) (0 <= score <= 96) ==>
Score = 10*(GPA + 2.8) + (MCAT - 500) (0 <= score <= 96) ==>
Score = 10*(GPA + 2.8 - 0.8) + (MCAT - 500) (0-10*0.8 <= score <= 96-10*0.8) ==>
Score = 10*(GPA + 2) + (MCAT - 500) (-8 <= score <= 88)

Score = 10*(GPA + 2) + (MCAT - 500) (-8 <= score <= 88)

So index shifting conserves the essential principles of simplicity and thoroughness by producing an easy metric with only a slightly expanded range.

Using the revised WedgeDawg-Lawper guidelines, we acquire the following:

Old 76 (i.e. 3.8/38 or 3.9/37) is new 80. This is generally the number to shoot for for top schools.

Old 73 (i.e. 3.8/35 or 3.9/34) is new 75. This is generally a good number for mid tiers while possibly being competitive for some top tiers.

Old 70 (i.e. 3.7/33 or 3.9/31) is new 70. This is generally where a "competitive" applicant for med school falls around.

Old 67 (i.e. 3.6/31 or 3.7/30) is new 65. This is around the accepted applicant median.

Old 65 (i.e. 3.6/29 or 3.7/28) is new 60. This is highly competitive for DOs and marginal for MD.

Data Analysis

Now, everyone likes data, so I decided to provide the necessary tables. For simplicity, the GPA range used was from 3.0 to 4.0, and the MCAT range used was from 500 to 528. It follows by extension for rest of the values, but this is SDN, so everyone should be in this range 😉 😛

Spoiler: Data Tables for Score-Mapping Model

Score-Mapping Model Table

AAMC Percentile Conversion Table

Percent Error Table

We can see from the above three tables that the score-mapping model isn't perfect, but the differences are mostly confined within <5% (the errors get worse for very low MCAT and GPA). The score-mapping model matches with the AAMC percentile data at average MCAT ranges (509-512) and at extremely high MCAT scores (>526).

Because the score-mapping model places a higher weight on the MCAT, it slightly punishes those with MCAT < 509, while slightly rewarding those with MCAT > 512. Much of the differences are addressed by AAMC's objective to de-emphasize the focus on the MCAT in favor of underlining the competency based requirements. For medical schools remain interested in numbers, the score-mapping model can be useful.

Also, below are the data tables of the simple metric.

Spoiler: Data Tables for WedgeDawg-Lawper Metric

WedgeDawg-Lawper Metric Table

Percent Error Table

I hope you find this new model to be interesting and helpful. Perhaps this new model is in fact inaccurate, but hey, it's fun exploring new possibilities.

Also, let me know if you find any mistakes here, and I will repair/reupload them.

---

Members don't see this ad.

 

[WedgeDawg]

I think the main advantage of the LizzyM score is that it's extremely easy to calculate and compare, so it's useful as a quick reference point. The more complicated we make it, the less useful it becomes. This is one instance where simplicity trumps accuracy, though of course both are necessary to some extent.

 

[NotASerialKiller]

So I decided to do something fun here.

😵

 

[Lawpy]

I think the main advantage of the LizzyM score is that it's extremely easy to calculate and compare, so it's useful as a quick reference point. The more complicated we make it, the less useful it becomes. This is one instance where simplicity trumps accuracy, though of course both are necessary to some extent.

Pfft. It's only just a fraction and a subtraction 😛

I agree, but keep in mind the complexity of LizzyM score is attributed to the complexity of the scale itself. Had the new MCAT ranged from 0 to 60, the LizzyM score would be 10*GPA + (45/60)*MCAT or 10*GPA + 0.75*MCAT. I think the AAMC made the scale for the new MCAT complex to discourage the over-emphasis of looking at numbers in favor of a competency-based evaluation. That's fine, but I would rather stick with the LizzyM score that we are familiar rather than creating a new score each time the new MCAT scale is out.

In fact, we can standardize the LizzyM formula for any given GPA scale and MCAT scale. It will look like this:

LizzyM = (40/GPA scale)*(GPA (on a given GPA scale)) + (45 / (highest new MCAT - lowest new MCAT)) * (MCAT - lowest new MCAT)

Trust me, it won't be any more complicated than this 😛 But at least the 0-85 point range is maintained regardless of whatever scale is being used.

 

[ImmunoLove]

huh?

 

[Lawpy]

huh?

Tl;dr: i devised a formula where the LizzyM score works for any arbitrary GPA and MCAT scales. It also generalizes WedgeDawg's model.

LizzyM scores will remain valid no matter what scoring scheme/rubric/scale the AAMC uses.

 

[ImmunoLove]

Tl;dr: i devised a formula where the LizzyM score works for any arbitrary GPA and MCAT scales. It also generalizes WedgeDawg's model.

LizzyM scores will remain valid no matter what scoring scheme/rubric/scale the AAMC uses.

🙂

 

[DoctorSynthesis]

Color Key: Blue = General Models, Red = Specific/Relevant/Contemporary Models

So I decided to do something fun here. Just to organize any theories, propositions, analyses etc. that I make, I will be calling them as Lawper Reports. This is different from my other threads regarding what I see in the news and miscellaneous things.

This report will focus on the famous LizzyM score and its role with the new 2015 MCAT.

Classical LizzyM Score

This is defined as LizzyM = 10*GPA + MCAT, where the GPA is out of a 4.0 scale and the MCAT is out of a 45 scale. Since the new MCAT is based on an entirely different scale (ranging from 472 to 528), the ideal and accurate approach is to use the AAMC Percentile Conversion Tables prepared by @efle.

After about few cycles (typically Class of 2022 and thereafter), the conversion tables lose much of their value as the old MCAT becomes obsolete. What happens to the LizzyM score?

WedgeDawg's Linear Extension Model

Developed by @WedgeDawg in Aug 2015 in the Continued Validity of LizzyM Scores thread, the proposed conversion is Score = 10*(GPA - 1) + (MCAT - 500). The model is called linear, since we are dealing with just basic addition and subtraction. WedgeDawg redefined the scoring system from the usual 85-point scale, to a new 58-point scale.

You can see his post described here (and in the above link):



Score-Conservation Model

WedgeDawg's model is great and accurate, but it raises some questions and concerns.

1. Why is the score range redefined from 0 to 85 to -32 to 58? It seems difficult to switch and adjust to the new scoring scheme after using the 0-85 scale for many years.

2. The LizzyM score has a slight preference to MCAT (GPA weighted out of 40 compared to MCAT weighted out of 45). The WedgeDawg score has a slight preference to GPA (GPA weighted out of 30 compared to MCAT weighted out of 28).

Note that WedgeDawg's model can be generalized as Score = 10*(GPA - a) + (MCAT - b), where a and b are appropriate parameters. However, these parameters are not chosen in random. Since the 2015 MCAT scale ranges from 472 and 528, the value of b is set to be the average of the two extremes, or b = 500. The parameter a is adjusted to ensure equal weights for GPA and MCAT.

I propose an alternative, slightly more complicated model that addresses the above two concerns, while following the similar derivation approach to WedgeDawg's model. The model is:

Score = 10*GPA + (old MCAT range)/(new MCAT range) * (MCAT - lowest new MCAT score)

This looks scary, so I will break it down:

new MCAT range = highest new MCAT score - lowest new MCAT score
old MCAT range = highest old MCAT score - lowest old MCAT score

The "new" and "old" terms are generalized and can be applied for any MCAT scale. For the 2015 MCAT, the model reduces to:

new MCAT range = 528 - 472 = 56
old MCAT range = 45 - 0 = 45

Score = 10*GPA + (45/56) * (MCAT - 472)

This model is also linear. The score becomes 0 for the lowest GPA and MCAT (0 and 472) and 85 for the highest GPA and MCAT (4 and 528), thus preserving the traditional LizzyM scoring range. Thus, the above model is MCAT-invariant. Likewise, the model prefers MCAT to GPA.

Now, everyone likes data, so I decided to provide the necessary tables. For simplicity, the GPA range used was from 3.0 to 4.0, and the MCAT range used was from 500 to 528. It follows by extension for rest of the values, but this is SDN, so everyone should be in this range 😉 😛

Score-Conservation Model Table

AAMC Percentile Conversion Table

Percent Error

We can see from the above three tables that the score-conservation model isn't perfect, but the differences are mostly confined within <5%. The score-conservation model matches with the AAMC percentile data at average MCAT ranges (509-512) and at extremely high MCAT scores (>526).

Because the score-conservation model places a higher weight on the MCAT, it slightly punishes those with MCAT < 509, while slightly rewarding those with MCAT > 512. Much of the differences are addressed by AAMC's objective to de-emphasize the focus on the MCAT in favor of underlining the competency based requirements. For medical schools remain interested in numbers, the score-conservation model can be useful.

I hope you find this new model to be interesting. I also stress that this model isn't a rejection to WedgeDawg's model (which I find it to be very useful and accurate), but a simple alternative that maintains the LizzyM score range of 0-85, with a slight preference for the MCAT. Perhaps this new model is in fact inaccurate, but hey, it's fun exploring new possibilities.

Also, let me know if you find any mistakes here, and I will repair/reupload them.

The point of lizzym is that it's simple and fairly accurate.

In my opinion just do GPA *100 + MCAT

Or GPA*10 + (MCAT-472)

Gives more weight to MCAT but the MCAT is more important anyway. Or we could just get rid of lizzym and just say your GPA and MCAT. There really is no need for lizzym scores. You can easily compare your GPA and MCAT to a school as you would compare your lizzym score to a schools lizzym score

 

[Lawpy]

The point of LizzyM is that it's simple and fairly accurate.

In my opinion just do GPA *100 + MCAT

Or GPA*10 + (MCAT-472)

Gives more weight to MCAT but the MCAT is more important anyway. Or we could just get rid of lizzym and just say your GPA and MCAT. There really is no need for lizzym scores. You can easily compare your GPA and MCAT to a school as you would compare your lizzym score to a schools lizzym score

I'm all for simplicity, but I'm also a supporter of LizzyM scores and I don't want them to be outdated just because of some random arbitrary scales. It was a useful reference for over a decade, so why stop suddenly or use another arbitrary scoring system?

I can very well simplify the original model to make it LizzyM = 10*GPA + 0.8*(MCAT - 472), because 45/56 is approximately equal to 0.8. Sure it may be slightly off, but it is still accurate. The LizzyM score by itself is a simple, linear equation. It is the complexity of the scales used that makes the LizzyM score seem daunting.

 

[Gandyy]

I've noticed that your GPA is not nearly as important as your MCAT in med school admissions. Someone with a 35 MCAT/3.5 GPA is in a much much better position than someone with a 3.9/28.

Since MCAT/GPA are the most important by far in med school admissions out of your entire application, (not saying EC's are not important), it cannot be overstressed as to how important it is that you be a really good standardized test taker.

Some people are good at standardized tests which helps them tremendously in admissions. Others are just bad at them no matter what which obviously hurts them a lot.

So basically MCAT > all other things on the application so LizzyM is a pretty good evaluator of your academics. Still a good analysis though Lawper.

 

[Lawpy]

Hey guys, I edited the OP to include the new LizzyM formulas in the spoiler. Just an early tl;dr 😉

I've noticed that your GPA is not nearly as important as your MCAT in med school admissions. Someone with a 35 MCAT/3.5 GPA is in a much much better position than someone with a 3.8/30

Yeah, I admit the MCAT-leaning bias, but I was just following the basis of the original LizzyM score. It has its flaws (like failing for those with GPA/MCAT splits, the 35/3.5 example you mentioned, etc.). And as I mentioned in the report, the new LizzyM score is a bit brutal to those with lower MCAT, while favoring those with higher MCAT.

I would just use it as an easy reference, while also keeping in mind that medical schools following the AAMC percentile guidelines will be much more forgiving than the new LizzyM calculation. For the numbers-hungry schools, well, the new LizzyM score satisfies their needs

 

[DoctorSynthesis]

I'm all for simplicity, but I'm also a supporter of LizzyM scores and I don't want them to be outdated just because of some random arbitrary scales. It was a useful reference for over a decade, so why stop suddenly or use another arbitrary scoring system?

I can very well simplify the original model to make it LizzyM = 10*GPA + 0.8*(MCAT - 472), because 45/56 is approximately equal to 0.8. Sure it may be slightly off, but it is still accurate. The LizzyM score by itself is a simple, linear equation. It is the complexity of the scales used that makes the LizzyM score seem daunting.

I think a good rule of thumb is once we have to start using calculators lizzym becomes pointless. If I was doing .8 times 511 I'm using a calculator.

Also all these scales are arbitrary as the mcat scale is arbitrary. Lizzym scores are a direct reflection on what the MCAT scale is. So if you want a basis for the scale that is it!

@LizzyM what say you?

 

[Lawpy]

I think a good rule of thumb is once we have to start using calculators LizzyM becomes pointless. If I was doing .8 times 511 I'm using a calculator.

Also all these scales are arbitrary as the mcat scale is arbitrary. Lizzym scores are a direct reflection on what the MCAT scale is. So if you want a basis for the scale that is it!

@LizzyM what say you?

Hmm, that is a good point. I'll see what I can do to fix things up. I was really just focusing on consistency and accuracy, but simplicity without using a calculator may require relaxing some of the rules.

 

[Lawpy]

Great news! I found a simple model that is also accurate (well <10% for the most part).

The simplified score-conserving model is: LizzyM = 10*(GPA + 2) + (MCAT - 500) = 10*GPA + (MCAT - 480)

This is slightly different from the WedgeDawg linear extension model (where we see a GPA - 1 term rather than GPA + 2 term), but I just rounded down the 2.25 to 2 and rounded 0.8 to 1. I was hesitant since it would damage the accuracy, but I was surprised!

Simplified Score-Conserving Model Table

Percent Error Table (using the AAMC Percentile Conversion Table listed in the first post)

So yes, the accuracy slightly worsened, but since the errors are less than 10% in the specified range, the model is suitable for use. The takeaway message is that do not be disheartened if you have a low MCAT. The revised LizzyM calculation is harsher than the AAMC conversion tables that medical schools use. The revised LizzyM score is just a metric to see where you stand and where you should apply in regards to academic stats. There are lots of factors involved in securing a medical school acceptance, so do not rely only on the LizzyM score.

I hope this revised model is helpful!

 

[LizzyM]

Please remember that the point is to find schools where your stats are a good match. Until we have data from schools as to the average MCAT of students who took the new MCAT, we really don't have a use for this new system. That said, the new system is elegant and the graphics seem worthy of a doctoral dissertation!

 

[feather421]

I've noticed that your GPA is not nearly as important as your MCAT in med school admissions. Someone with a 35 MCAT/3.5 GPA is in a much much better position than someone with a 3.9/28.

Since MCAT/GPA are the most important by far in med school admissions out of your entire application, (not saying EC's are not important), it cannot be overstressed as to how important it is that you be a really good standardized test taker.

Some people are good at standardized tests which helps them tremendously in admissions. Others are just bad at them no matter what which obviously hurts them a lot.

So basically MCAT > all other things on the application so LizzyM is a pretty good evaluator of your academics. Still a good analysis though Lawper.

Have you seen the table where admissions officers rank the things that are important to them? After the interview, the MCAT (theoretically) drops down in importance behind things like LORs and your actual interview.

 

[RaspberrySlushy]

I like that this keeps the old scale. Been reading here for awhile and there's so much based on the old scale that I like that you made a formula to fit new MCAT scores into the old scale!

 

[Gandyy]

Have you seen the table where admissions officers rank the things that are important to them? After the interview, the MCAT (theoretically) drops down in importance behind things like LORs and your actual interview.

Yea, thats AFTER the interview though. You have to have the MCAT to get the interview. Before the interview, its the most important thing.

 

[Lawpy]

Please remember that the point is to find schools where your stats are a good match. Until we have data from schools as to the average MCAT of students who took the new MCAT, we really don't have a use for this new system. That said, the new system is elegant and the graphics seem worthy of a doctoral dissertation!

I understand and it does seem rather early. However, i just prepared a safe defense in anticipation for major changes to be seen in the future, since i wouldn't like to see your famous scoring metric being tossed aside after its long and essential usage.

 

[WedgeDawg]

Another easy estimation you can use is (GPA*10)+(MCAT-482) which works for the MCAT range of 30-39 (509-523) which is the important distinguishing range and the numbers in that range match up fairly well (the 512-521 range is the most accurate, which is 31ish-38 old MCAT). This works well within this range for all GPA values. MCAT scores above 523 are iffy, but then the LizzyM score breaks down anyway for extreme values.

Values assume 4.0 GPA
Old  New Old New   Split
39   523  81  79     2
     522  80  78     2
38   521  79  78     1
     520  78  77     1
37   519  77  77     0
36   518  76  76     0
35   517  75  75     0
34   516  74  74     0
     515  73  73     0
33   514  72  73     1
32   513  71  72     1
     512  70  71     1
     511  69  71     2
31   510  68  71     3
30   509  67  70     3

 

[WedgeDawg]

Alternatively, here's a simple javascript calculator for Lawper's version so that you don't even have to do the math. Just plug and chug and you're good.

Calculator

 

[Lawpy]

Another easy estimation you can use is (GPA*10)+(MCAT-482) which works for the MCAT range of 30-39 (509-523) which is the important distinguishing range and the numbers in that range match up fairly well (the 512-521 range is the most accurate, which is 31ish-38 old MCAT). This works well within this range for all GPA values. MCAT scores above 523 are iffy, but then the LizzyM score breaks down anyway for extreme values.

Values assume 4.0 GPA
Old  New Old New   Split
39   523  81  79     2
     522  80  78     2
38   521  79  78     1
     520  78  77     1
37   519  77  77     0
36   518  76  76     0
35   517  75  75     0
34   516  74  74     0
     515  73  73     0
33   514  72  73     1
32   513  71  72     1
     512  70  71     1
     511  69  71     2
31   510  68  71     3
30   509  67  70     3

Ok thanks! I will probably use that since the boundaries are closer to the old LizzyM score (-10 to 86, compared to -8 to 88 in the other simple model).

The only downside is that it is arranged to be slightly complex (subtracting from 482 can be weird). It can be rearranged like 10*(GPA+1.8)+(MCAT-500), so it can help.

Alternatively, here's a simple javascript calculator for Lawper's version so that you don't even have to do the math. Just plug and chug and you're good.

Calculator

Good work thanks.