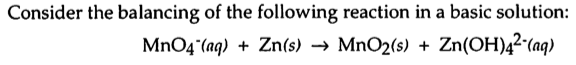Yeah, that was a typo in an older edition of the general chemistry book.
Sorry to be the bringer of bad news, but if you look at your final balanced equation, it's not quite right. You show 3 Zn, 2 Mn, 16 O, 16 H, and a -2 charge on the left side and 3 Zn, 2 Mn, 20 O, 16 H, and a -10 charge on the right side.
The balance equation should be:
3Zn + 2MnO4^- + 4OH^- + 4H2O ----> 2MnO2 + 3Zn(OH)4^2-
But truth be told, when it comes to balancing questions, you should look for the reductant/oxidant ratio and then look at the answer choices with the correct ratio and eliminate the ones that are not correctly balanced (either wrong number of atoms on each side or an imbalance of charges on each side). Balancing from scratch would not be the best use of a test taker's time.