- Joined
- Apr 17, 2010
- Messages
- 377
- Reaction score
- 48
Could someone please explain the math behind this? I'm unclear on how x is solved for below.
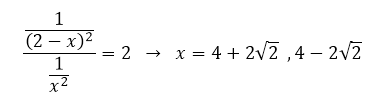
Thanks!
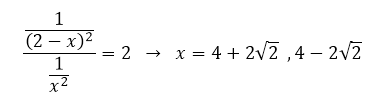
Thanks!
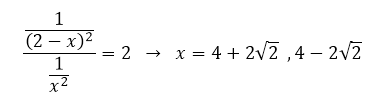
I never use the quadratic equation. Completing the square works every time if you can't factor a simpler way.
The equation simplifies a bit to
x^2 - 8x = -8
Once in this format, you can complete the square: basically add (b/2)^2 to both sides of the equation to get
x^2 - 8x + 16 = 8
Now the left side easily factors to
(x - 4)^2 = 8
Take the square root of both sides
x - 4 = (+/-)2*sqroot(2)
Which simplifies to your answer.
Quick instructions to complete the square:
1. write the equation in the form ax^2 + bx = c
2. if a is anything other than 1, divide each term by a to remove the coefficient
3. add (b/2)^2 to both sides of the equation
4. factor the left side: (it will factor to (x + (b/2))^2)
5. take the square root of both sides and simplify to get your answer.
I never use the quadratic equation. Completing the square works every time if you can't factor a simpler way.
The equation simplifies a bit to
x^2 - 8x = -8
Once in this format, you can complete the square: basically add (b/2)^2 to both sides of the equation to get
x^2 - 8x + 16 = 8
Now the left side easily factors to
(x - 4)^2 = 8
Take the square root of both sides
x - 4 = (+/-)2*sqroot(2)
Which simplifies to your answer.
Quick instructions to complete the square:
1. write the equation in the form ax^2 + bx = c
2. if a is anything other than 1, divide each term by a to remove the coefficient
3. add (b/2)^2 to both sides of the equation
4. factor the left side: (it will factor to (x + (b/2))^2)
5. take the square root of both sides and simplify to get your answer.
