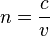Dispersion of light through a prism

[km1865]

---

Members don't see this ad.

So according to TBR, a light ray of higher frequency will refract more than a light of a lower frequency (so the higher frequency ray has a higher n). This doesnt make sense to me, since n= c/v; v=lamda f, then isnt it that n= c/(lamda* f)? Therefore, isnt what TBR is saying incorrect, since the higher frequency light ray should have a lower n , since n and f are indirectly related?

Also Im a little confused about the n value of the light, in my book it says that the ray that bends more has a higher n value.. why is this so? I thought n was a property of the MEDIUM and not of the light ray itself?

And just to clarify, I thought that the wave that refracts more (if it really does have a higher n value?), according to v=lamda* f, will also have a lower velocity and wavelength as well? We keep the frequency of the ray constant becuase it is dependent on the original energy source of the wave, and so it does not depend on medium properties like wavelength and velocity, right?

Thanks alot for clearing up these ideas!

 

[MD Odyssey]

Also Im a little confused about the n value of the light, in my book it says that the ray that bends more has a higher n value.. why is this so? I thought n was a property of the MEDIUM and not of the light ray itself?

As it turns out, n is actually dependent upon the frequency of the incoming light. This is often confusing for the reasons you've mentioned, since textbooks are really only telling you part of the story. I'll try to elaborate a bit.

Consider light as a stream of photons. As a photon enters a medium, such as glass, it gets absorbed by the atoms in the material. Those atoms then re-emit the light in a random direction where they are absorbed once again by atoms in the material. This cycle of absorption, re-emission continues until the photons have exited the medium out the other side. If you divide the length of your medium by the time required for it to transit that medium, you can find the effective velocity of the photons through the material.

However, I need to emphasize the fact that the speed of light is still a constant - light can only exist at a speed of c. What's really going on is that light is not traveling a straight line, therefore the perceived propagation speed is lower. The index of refraction is defined as the ratio

Since the absorption characteristics depend on the energy of the photons (i.e., some energies have lower likelihoods of absorption), the term in the denominator is in general a function of frequency, which explains why prisms separate light by frequency.

There is an alternate explanation which can be used to explain this by considering light as a wave rather than a particle, as I have done here. However, I don't understand it as well as I would like and the parts that I do understand are very complicated. This is what BR is somewhat glossing over.

I've written about this before here.
​

 

[KindOfMaroon]

I like your questioning of the following equations:

n= c/v1; v2=lamda f, then isnt it that n= c/(lamda* f)

The first v is the velocity of light in the refractory material (glass, water, etc.) The second v is a general equation for the velocity of waves, which is dependent upon their wavelength and frequency. So, if we use your second equation: n= c/l*f, then shouldn't a larger f yield a lower n? It would seem so, if we substitute these equations. The problem is v1 is not purely determined by the wavelength and frequency of the light, but also by the material the light is in! Thus, v2 is not entirely the same as v1.

Think about a prism: it disperses light of different colors (i.e. different frequencies). This is due to the process of absorption and reemission that occurs. The light wave is essentially running into atom after atom, being absorbed and reemitted constantly. The higher frequencies of light lose more measurable velocity during this process due to time spent being absorbed/reemitted. Thus, they will "slow down" more on a large scale, but on the microscopic scale, of course c is constant.

So, I think there are slight problems in assumption going on here. Anyone feel free to correct me if I'm totally off track 😀

 

[vayntraubinator]

v = Frequency * wavelength

Changing between medium, frequency remains constant.

Therefore, only the wavelength changes when entering a new medium.

The index of refraction is defined as n = c / v
and this ratio will always be greater than one since light will travel fastest in the speed of light of a vacuum.

Therefore, thinking about the change in wavelength and velocity as a light ray enters a new medium, we must examine the medium in which it was in, and the medium in which it entered.

Intuitively, light travels faster in air than in water. This relationship helps illustrate why the index of refraction then increases going from air to water. It's because the denominator of (c/v) is getting smaller, therefore increasing n.

Hence, when n of source Medium (Ms) < n of final Medium the velocity will decrease and by the equation v=f*lambda, lambda will decrease since frequency remains constant.

Similarly, when n of Ms > n of Mf the velocity will increase and hence, lambda will increase. This is the situation for light going from water, to the air.



With regards to degree of change when entering a new medium (chromatic dispersion) know that higher wavelength(lower frequencies) travel faster through a medium than shorter wavelengths(higher frequencies), so the higher wavelength bends less dramatically at the media interface.

If you think of a car with 2 front wheels entering a new medium at an angle, one of the axles will remain in contact with the medium longer than the other as the car bends towards the new medium.

For me, for differing frequencies of the same velocity, I think of higher frequency meaning longer contact at the moment of turning, so a greater degree of bending for a higher frequency.

Hope dat helps😕👍

 

[km1865]

Hence, when n of source Medium (Ms) < n of final Medium the velocity will decrease and by the equation v=f*lambda, lambda will increase since frequency remains constant.

Similarly, when n of Ms > n of Mf the velocity will increase and hence, lambda will decrease. This is the situation for light going from water, to the air.

But for the first situation, where n source < n final, wouldn't the wavelength decrease if velocity decreases, since frequency is constant? Why are they indirectly related? Same for the second situation, if velocity increases, then lamda should increase holding f constant?

With regards to degree of change when entering a new medium (chromatic dispersion) know that higher wavelength(lower frequencies) travel faster through a medium than shorter wavelengths(higher frequencies), so the higher wavelength bends less dramatically at the media interface.

Is there a reason why this happens? I'm still confused about this, doesn't this contradict that a higher frequency= longer amount of contact, therefore shouldn't the higher frequency travel at slower speeds, relatively of course?

Also, can I just explain bending deviations using snell's law, a decreasing wavelength means an increasing index of refraction, leading to increased bending, so increasing the index of refraction would actually decrease theta(final) acording to snells law. therefore theta has CHANGED/deviated from theta initial (right when it was incident to the prism) to theta final (when it comes out of the prism)..

Thanks so much! Clarifying these concepts really helps, this stuff is bothering/confusing me! =/

 

[km1865]

nvm, got it thanks everyone! I was just thinkingabout the equation in the wrong way lol