EK 1001 Physics - Answer key wrong?

[frog301]

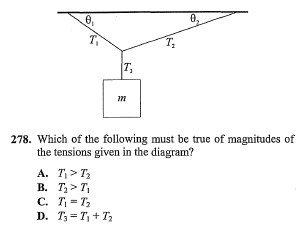
#278 from EK 1001 Physics.

In this one, the magnitude of angles are unknown, and are assuming the system is in equilibrium.
Therefore, looking at horizontal aspects of T1 and T2 you can set T1cos(theta) = T2cos(theta). Cancel out cos(theta) to get T1=T2.

Am I missing something here? I don't understand where in the world they pulled out T1>T2

---

Members don't see this ad.

 

[AdaptPrep]

Hi, frog301--

You do have the correct equation, but remember, you can only cancel cos(theta) if the angles are equal. In this problem, the angles are not equal, so you cannot cancel them. Therefore, we know T1 cannot equal T2 (option C is, therefore, incorrect).

I find it easier to look at the y-component of each tension (both are positive values since they are directed upwards to keep the crate in equilibrium):

(T1) sin(theta1) and (T2) sin(theta2)

Those two values added together must equal the weight force of the crate (mg or T3):

(T1) sin(theta1) + (T2) sin(theta2) = T3 (this is why option D is incorrect)

Which ever angle is larger will be contributing more tension to hold the crate in equilibrium. The take home lesson is: the larger angle has the higher tension. Or, whichever rope is closest to hanging vertical has the highest tension. It is easier to understand that than doing the math.

 

[frog301]

Hi, frog301--

You do have the correct equation, but remember, you can only cancel cos(theta) if the angles are equal. In this problem, the angles are not equal, so you cannot cancel them. Therefore, we know T1 cannot equal T2 (option C is, therefore, incorrect).

I find it easier to look at the y-component of each tension (both are positive values since they are directed upwards to keep the crate in equilibrium):

(T1) sin(theta1) and (T2) sin(theta2)

Those two values added together must equal the weight force of the crate (mg or T3):

(T1) sin(theta1) + (T2) sin(theta2) = T3 (this is why option D is incorrect)

Which ever angle is larger will be contributing more tension to hold the crate in equilibrium. The take home lesson is: the larger angle has the higher tension. Or, whichever rope is closest to hanging vertical has the highest tension. It is easier to understand that than doing the math.

Thank you!