Ok, I will explain it exactly. The statement is actually an inequality: delta_position*delta_momentum > h/4*pi where h is planck's constant.
This is how it goes down. You've probably heard of wave-particle duality that says that all particles have wave-like properties or vice versa. In reality objects are neither waves nor particles but have a mix of properties that we associate with both.
So, you are familiar with the fact that the frequency of a wave is related to its energy by E=hf. Momentum is also related to properties of a wave(it's wavelength) by this equation where p stands for momentum:
.
Now, if a particle can be described by a wave then what property of the wave is related to its position? Well, the obvious guess is that the location of the wave is related to the location of the particle. If you find the wave the particle will be there! So the position of the particle is given by the location of the wave itself.
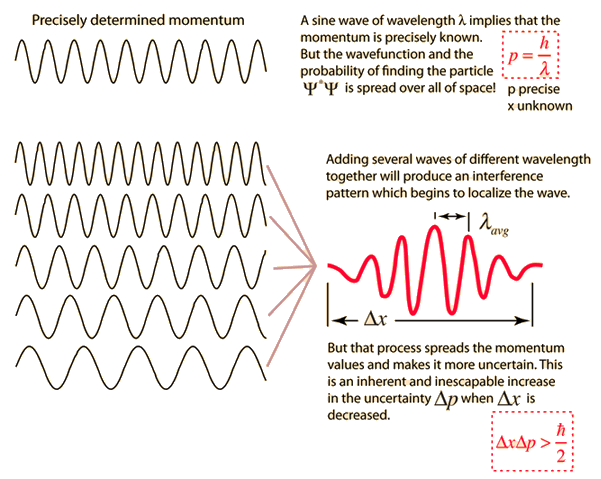
So a particle traveling through space would have a wave that looks sort of like the wave on the right with the lines going flat on both sides. :
So what does this have to do with uncertainty? Well, if you have a wave that starts and ends like the wave above you can't precisely define it's wavelength because its changing from peak to trough. But you DON'T run into this problem if you have a wave that looks like any one of the ones on the left.
All these waves have precisely defined wavelengths because they never start or stop. So the only way to know the momentum precisely is if you say that the wave goes forever which means you have no idea where the particle is located. It could be anywhere! But if you try to trap the particle in a region in space then it's wavelength changes every peak to trough so you don't have a precise wavelength for it...which means you don't know the momentum precisely!
From this strange behavior you can reach the conclusion mathematically that the particle's position and momentum are related with a precise amount of uncertainty.
This is only one way of looking at it--the wave way. You can describe quantum mechanics in tons of ways including the matrix way. You can reach the same conclusion using matrix mathematics. If you go even deeper to quantum electrodynamics(graduate physics stuff) you would see that you can do away with the wave and matrix interpretation altogether and use something called path integrals and come up with a completely different interpretation of uncertainty. I won't go further but a layman's book on the topic that is incredibly short and requires no mathematics is called "QED : The Strange Theory of Light and Matter" by Richard Feynman.
Additional Info: If you look at the DeBroglie equation you might make the clever insight that DeBroglie did so long ago that anything that has momentum has a wavelength. So a basketball has a wavelength associated with it in proportion to its momentum. That means that basketballs exhibit all sorts of phenomenon that you can't see because the phenomenon is so small. One property would be that basketballs can diffract because waves diffract. You would be able to see this if planck's constant were larger...but it's actually very small and 'close' to 0. Ok, time to stop nerding out here.