- Joined
- May 25, 2018
- Messages
- 131
- Reaction score
- 153
I do not understand how they got 'A' as the answer.
Here's how I initially tackled the problem, which turned out to be so unnecessarily confusing.
Solved for acceleration first (gsin30=5).
a=5
Solved for t going down ramp. 10=1/2at^2 -> t=sqrt(10(2)/a) -> t=sqrt(4)=2 seconds
Solved for Vf. Vf+Vi/2=d/t -> Vf=(10/2)(2) - 0 = 10 m/s
Now b/c we know regarding inclined plane, a=gsin(theta). At the bottom of the ramp, theta=0 or 180. sin0=0, meaning no change in velocity.
So with constant velocity at the bottom of the ramp, to travel distance 'x' the Vi=Vf, because it doesn't change due to 0 acceleration.
Vf+Vi/2=d/t. 10+10/2=10/t. t=10/10= 1 second to travel 'x' distance.
Did I do this problem correctly? I know I got the right answer, but unsure if my logic using constant velocity due to a=0 from gsin(0) was correct when I solved for time to travel 'x' distance.
*answer is A btw

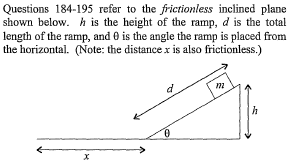
Here's how I initially tackled the problem, which turned out to be so unnecessarily confusing.
Solved for acceleration first (gsin30=5).
a=5
Solved for t going down ramp. 10=1/2at^2 -> t=sqrt(10(2)/a) -> t=sqrt(4)=2 seconds
Solved for Vf. Vf+Vi/2=d/t -> Vf=(10/2)(2) - 0 = 10 m/s
Now b/c we know regarding inclined plane, a=gsin(theta). At the bottom of the ramp, theta=0 or 180. sin0=0, meaning no change in velocity.
So with constant velocity at the bottom of the ramp, to travel distance 'x' the Vi=Vf, because it doesn't change due to 0 acceleration.
Vf+Vi/2=d/t. 10+10/2=10/t. t=10/10= 1 second to travel 'x' distance.
Did I do this problem correctly? I know I got the right answer, but unsure if my logic using constant velocity due to a=0 from gsin(0) was correct when I solved for time to travel 'x' distance.
*answer is A btw
