Physics - Circular Motion and Rollercoasters

[Aletheia]

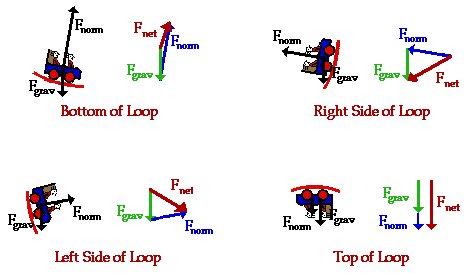
Just a basic question. I was looking over some rollercoaster physics problems and trying to determine the FN after you determine the net force. So, at the bottom of the coaster, the Fgrav force is pushing down on the object and the FN forces are pushing up. Does this mean that Fnet= negativeFgrav+FN??? The reason I'm confused is that I looked at two different examples outlining this concept and one of them had that, but the other had Fnet=Fgrav+FN so now I'm really confused. Would you account for the fact that they are opposing forces like that and, essentially, end up with Fnet+Fgrav=FN OR would it be Fnet-Fgrav=FN.

Thanks!

---

Members don't see this ad.

 

[RogueUnicorn]

it all depends on how you define the forces (their vectors)

 

[Isoprop]

 

[snoopypoo]

I wanted to start a new thread because it was only somewhat related to this question. However, I am have problems starting a thread. Hopefully this works:

I find my understanding of this problem seemingly contradictory of centripetal force.

Aren't these two always true about Fc
1. Objects moving at circle have net force = mv^2/r
2. that this net force points towards the center

However in doing Berkeley and the problem with roller coasters, I am confused. The problem states poorly paraphrased as such :what is the direction of the net force when a roller coaster is at lets say point B traveling through a loop. If the loop is a clock point B is 3 o clock.

or "right side of the loop in above picture"

Solution states that with mg pointing down and normal force pointing towrad the center, that the net force is pointing toward 6oclock. This answer must contradict statements 1 or 2 above. Right?

 

[Isoprop]

I wanted to start a new thread because it was only somewhat related to this question. However, I am have problems starting a thread. Hopefully this works:

I find my understanding of this problem seemingly contradictory of centripetal force.

Aren't these two always true about Fc
1. Objects moving at circle have net force = mv^2/r
2. that this net force points towards the center

However in doing Berkeley and the problem with roller coasters, I am confused. The problem states poorly paraphrased as such :what is the direction of the net force when a roller coaster is at lets say point B traveling through a loop. If the loop is a clock point B is 3 o clock.

or "right side of the loop in above picture"

Solution states that with mg pointing down and normal force pointing towrad the center, that the net force is pointing toward 6oclock. This answer must contradict statements 1 or 2 above. Right?

You seem to misunderstand the meaning of a net force. Net forces are when you add up all the forces. Centripetal force is one of the forces in this problem that you must add up.

Statements 1 and 2 are true for centrip force, NOT the total (net) force of an object. And centrip force isn't the only force acting on this problem. The problem was asking for the NET force. You have two forces, centrip and gravitational. When you add both forces up, you get the net force.

Think of it as a ramp problem. It's true that gravitational force is always (1) equal to mg; and (2) pointing downwards. So what is the net force on a box sliding down a ramp? You add up gravitational force, frictional force, and the normal force of the ramp to get the net force.

 

[snoopypoo]

You seem to misunderstand the meaning of a net force. Net forces are when you add up all the forces. Centripetal force is one of the forces in this problem that you must add up.

Statements 1 and 2 are true for centrip force, NOT the total (net) force of an object. And centrip force isn't the only force acting on this problem. The problem was asking for the NET force. You have two forces, centrip and gravitational. When you add both forces up, you get the net force.

Think of it as a ramp problem. It's true that gravitational force is always (1) equal to mg; and (2) pointing downwards. So what is the net force on a box sliding down a ramp? You add up gravitational force, frictional force, and the normal force of the ramp to get the net force.

so you're saying centripetal force is not always the net force? but that in itself it does point toward the center. I asked because in other problems with objects moving in circular motion, the net force WAS equated to Fc.

 

[godcyning]

Fnet is the sum of all the forces, always. SUM.

The first replier directly answered your question but I'll elaborate...it depends on how you define your force vectors.

So at the BOTTOM of the coaster (i.e. on a flat track), it JUST SO HAPPENS that the normal and gravitational forces are equal and pointing in exactly opposite directions. The net force is zero. Whoever said net was normal + gravitational was defining gravitational as a negative value, since it was pointing down, whereas normal pointing up is positive. Whoever said that net = normal - gravitational was using the magnitude of the gravitational force, without the negative sign. It comes down to convention, whether you prefer to add a negative or to subtract a positive. But draw it out...always...and the arrows will never lie.

 

[Isoprop]

so you're saying centripetal force is not always the net force? but that in itself it does point toward the center. I asked because in other problems with objects moving in circular motion, the net force WAS equated to Fc.

Well in some physics problems, you will be told that there is a complex mixture of forces but the overall motion of the object is a uniform circular motion. Then you know the net force will be the same as mv^2/r.

For example, let's say I have a hockey puck on the ground and there are three people pushing on the puck in different directions. The hockey puck is going in a circle with constant speed. There are a bunch of forces acting on the puck: gravity, normal force of the ground, the three forces of the people. But because the net motion is a uniform circle, we know that the net force is mv^2/r.

For the rollarcoaster, the net motino of the train isn't in uniform circular motion because the train slows down at the top and speeds up at the bottom.

In the end, you have to analyze the situation.

 

[snoopypoo]

Well in some physics problems, you will be told that there is a complex mixture of forces but the overall motion of the object is a uniform circular motion. Then you know the net force will be the same as mv^2/r.

For example, let's say I have a hockey puck on the ground and there are three people pushing on the puck in different directions. The hockey puck is going in a circle with constant speed. There are a bunch of forces acting on the puck: gravity, normal force of the ground, the three forces of the people. But because the net motion is a uniform circle, we know that the net force is mv^2/r.

For the rollarcoaster, the net motino of the train isn't in uniform circular motion because the train slows down at the top and speeds up at the bottom.

In the end, you have to analyze the situation.

THAT IS EXACTLY what i was looking for. THANK YOU!
also, given that, is it the fact that the object is moving in a circular albiet not at uniform accelaration the reason we use the formula, mv^2/r

 

[godcyning]

also, given that, is it the fact that the object is moving in a circular albiet not at uniform accelaration the reason we use the formula, mv^2/r

well... Fc = mv^2/r is valid for anything moving in a circle, uniform speed or not.

since speed is changing (i.e. not uniform), Fc is changing also, Fc being the component of the net force pointed toward the middle of the circle. There's gonna be another component of the net force that's tangential to the circle, which is responsible for the speed changing.

 

[snoopypoo]

well... Fc = mv^2/r is valid for anything moving in a circle, uniform speed or not.

since speed is changing (i.e. not uniform), Fc is changing also, Fc being the component of the net force pointed toward the middle of the circle. There's gonna be another component of the net force that's tangential to the circle, which is responsible for the speed changing.

yes now I understand. Thank you.
anything moving in a curve path has angular acceleration = v^2/r

 

[RogueUnicorn]

anything moving in a circular curved path has that angular acceleration formula... curves can be spirals as well