Why does frequency remain the same?

[zoner]

---

Members do not see this ad.

I never understood why when I was taking Phy II. Why does frequency of light remain the same when going through a medium such as water or prism but other variables such as velocity or wavelength can change?

 

[justhanging]

I never understood why when I was taking Phy II. Why does frequency of light remain the same when going through a medium such as water or prism but other variables such as velocity or wavelength can change?[/QUOT]

Because it can't, otherwise the energy would change when traveling through different mediums which doesn't make sense.

E = hf

If frequency changed energy would change and the energy of light doesn't change when traveling in different mediums. But since the speed changes something has to change which is wavelength. If wavelength changes energy doesn't change because speed is also part of the equation.

E = hv/lamda

When the speed changes the wavelength changes accordingly to keep energy constant.

 

[lolarogers]

That's impossible, i think. If wavelength changes, then frequency MUST change. Mathematically, they're indirectly proportional.

 

[MedChallenge]

I'm pretty confused about when velocity, frequency, wavelength and energy change for both sound and EM waves. I know there's the rule that frequency of a wave doesn't change based on the medium it goes through...but the velocity does. This implies that the wavelength changes. Is this for light or sound?

Can someone clear up in which situations these properties change? And what else do I need to know about these properties for the test? I know this may be hard to do when not in person, but I would appreciate as little or as much help as anyone is willing to offer!

 

[whiteshadodw]

I'm pretty confused about when velocity, frequency, wavelength and energy change for both sound and EM waves. I know there's the rule that frequency of a wave doesn't change based on the medium it goes through...but the velocity does. This implies that the wavelength changes. Is this for light or sound?

Can someone clear up in which situations these properties change? And what else do I need to know about these properties for the test? I know this may be hard to do when not in person, but I would appreciate as little or as much help as anyone is willing to offer!

v=wavelength*f

lets say sunlight goes from air to a prism. inside the prism, light has a greater speed. the photons all of a sudden got faster, but if their frequency changed then they would have somehow picked up energy magically. remember, from the conservation of energy, you can't just create energy out of nowhere. however, by changing the wavelength of this photon and keeping the frequency the same you have now changed the velocity:

wavelength 1 = 1 m frequency 1 = 1 Hz (cycle/sec)
velocity 1 = wavelength 1 (1m) * frequency 1 (1/s) = 1 m/s

wavelength 2 = 2 m frequency 2 = 1 Hz (cycle/s)
velocity 1 = wavelength 2 (2m) * frequency 2 (1/s) = 2 m/s

we've changed the speed of this 'photon' two fold due to a medium switch without adding more energy into the photon. the wavelength changes between mediums is actually what causes refraction of light and the fact that sunlight that goes through a prism comes out split into the colors of the rainbow. this holds true for all EM radiation AND sound.

also, consider this, when a light of one frequency passes through a prism or glass or something, the light doesn't change color. it is refracted because the wavelength changes, and that's all. our eyes are sensitive to frequency of light, therefore if you send blue light through a prism, you get blue light out of the prism. the frequency hasn't changed, but the wavelength has, and hence the refraction.

 

[MedChallenge]

Thanks for that explanation, whiteshadodw! Do I have this correct: because E=hf, frequency can only change (in ANY type of wave) if energy is added or removed?

To follow-up, you never mentioned a time when frequency changes. So how is this different from observed frequency in the doppler effect, which obviously does change based on the speeds of the detector or source? How does wavelength fit into the doppler effect?

v=wavelength*f

lets say sunlight goes from air to a prism. inside the prism, light has a greater speed. the photons all of a sudden got faster, but if their frequency changed then they would have somehow picked up energy magically. remember, from the conservation of energy, you can't just create energy out of nowhere. however, by changing the wavelength of this photon and keeping the frequency the same you have now changed the velocity:

wavelength 1 = 1 m frequency 1 = 1 Hz (cycle/sec)
velocity 1 = wavelength 1 (1m) * frequency 1 (1/s) = 1 m/s

wavelength 2 = 2 m frequency 2 = 1 Hz (cycle/s)
velocity 1 = wavelength 2 (2m) * frequency 2 (1/s) = 2 m/s

we've changed the speed of this 'photon' two fold due to a medium switch without adding more energy into the photon. the wavelength changes between mediums is actually what causes refraction of light and the fact that sunlight that goes through a prism comes out split into the colors of the rainbow. this holds true for all EM radiation AND sound.

also, consider this, when a light of one frequency passes through a prism or glass or something, the light doesn't change color. it is refracted because the wavelength changes, and that's all. our eyes are sensitive to frequency of light, therefore if you send blue light through a prism, you get blue light out of the prism. the frequency hasn't changed, but the wavelength has, and hence the refraction.

 

[whiteshadodw]

Thanks for that explanation, whiteshadodw! Do I have this correct: because E=hf, frequency can only change (in ANY type of wave) if energy is added or removed?

To follow-up, you never mentioned a time when frequency changes. So how is this different from observed frequency in the doppler effect, which obviously does change based on the speeds of the detector or source? How does wavelength fit into the doppler effect?

Yeah, I forgot Dopler effect, but I think that's a little different since I think technically the speed of sound isn't changing. Speed of sound has to be constant in a medium regardless of intensity or frequency or wavelength. In the Dopler effect the sound isn't changing medium, so therefore if wavelength changes then frequency changes as well. So in this situation yes, both change. However, because there is no medium change, frequency and wavelength both change in order for speed of sound in that medium to remain the same.

 

[MT Headed]

Thanks for that explanation, whiteshadodw! Do I have this correct: because E=hf, frequency can only change (in ANY type of wave) if energy is added or removed?

To follow-up, you never mentioned a time when frequency changes. So how is this different from observed frequency in the doppler effect, which obviously does change based on the speeds of the detector or source? How does wavelength fit into the doppler effect?

E=hf only holds for measuring the energy of photons. Don't try to apply it to sound, or waves on a string.

The doppler effect does not change anything. Photons exhibit a doppler effect too, that is how we get radar guns and doppler weather radar. The frequency and the wavelength of light will change as two objects approach each other or go apart from each other. This is a very different phenomena than light going from one medium to another (because a new medium implies a new speed of light).

 

[whiteshadodw]

E=hf only holds for measuring the energy of photons. Don't try to apply it to sound, or waves on a string.

The doppler effect does not change anything. Photons exhibit a doppler effect too, that is how we get radar guns and doppler weather radar. The frequency and the wavelength of light will change as two objects approach each other or go apart from each other. This is a very different phenomena than light going from one medium to another (because a new medium implies a new speed of light).

you're right that E=hf only holds true for photons. however, light and sound and any sort of wave still has an energy associated with it. so while that equation doesn't hold true, the idea that energy remains constant is true.

 

[MedChallenge]

Thanks guys, I'm getting a much better understanding already and would appreciate clearing up the following:

If the speed of any wave is constant in the same medium, why does the frequency and wavelength change when a detector and source are in motion toward/away from each other? I guess what I'm lacking is a fundamental understanding of frequency and wavelength and how you know that those change for a constant speed of sound? That implies an energy change, as well, so where does that energy come from? I understand that changing frequency and wavelength can keep a constant velocity, but what I don't understand is why it does that.

 

[whiteshadodw]

Thanks guys, I'm getting a much better understanding already and would appreciate clearing up the following:

If the speed of any wave is constant in the same medium, why does the frequency and wavelength change when a detector and source are in motion toward/away from each other? I guess what I'm lacking is a fundamental understanding of frequency and wavelength and how you know that those change for a constant speed of sound? That implies an energy change, as well, so where does that energy come from? I understand that changing frequency and wavelength can keep a constant velocity, but what I don't understand is why it does that.

that is the "Doppler Effect" and i feel like the wiki page does a good job of explaining it:

The relative increase in frequency can be explained as follows. When the source of the waves is moving toward the observer, each successive wave crest is emitted from a position closer to the observer than the previous wave. Therefore each wave takes slightly less time to reach the observer than the previous wave. Therefore the time between the arrival of successive wave crests at the observer is reduced, causing an increase in the frequency. While they are travelling, the distance between successive wavefronts is reduced; so the waves "bunch together". Conversely, if the source of waves is moving away from the observer, each wave is emitted from a position farther from the observer than the previous wave, so the arrival time between successive waves is increased, reducing the frequency. The distance between successive wavefronts is increased, so the waves "spread out".

 

[ThirdEye]

Thanks guys, I'm getting a much better understanding already and would appreciate clearing up the following:

If the speed of any wave is constant in the same medium, why does the frequency and wavelength change when a detector and source are in motion toward/away from each other? I guess what I'm lacking is a fundamental understanding of frequency and wavelength and how you know that those change for a constant speed of sound? That implies an energy change, as well, so where does that energy come from? I understand that changing frequency and wavelength can keep a constant velocity, but what I don't understand is why it does that.

I've been in the same boat as you were but I think I have it figured out finally. The missing info on all of this is that the emitted frequency doesn't change! It's the perceived frequency that changes, as well as wavelength.

 

[Donald Juan]

that is the "Doppler Effect" and i feel like the wiki page does a good job of explaining it:

The relative increase in frequency can be explained as follows. When the source of the waves is moving toward the observer, each successive wave crest is emitted from a position closer to the observer than the previous wave. Therefore each wave takes slightly less time to reach the observer than the previous wave. Therefore the time between the arrival of successive wave crests at the observer is reduced, causing an increase in the frequency. While they are travelling, the distance between successive wavefronts is reduced; so the waves "bunch together". Conversely, if the source of waves is moving away from the observer, each wave is emitted from a position farther from the observer than the previous wave, so the arrival time between successive waves is increased, reducing the frequency. The distance between successive wavefronts is increased, so the waves "spread out".

Just to piggy back off of that, it is usually easy to picture the doppler effect by imagining yourself walking out into the ocean, when you are going toward the waves, they hit you more often (increased frequency). when you are moving in the same direction as the waves, they hit you less often (decreased frequency). Also, keep in mind though that the doppler effect is only a change in the perceived frequency, and not an actual change in the frequency.

 

[Labminion]

I hope the original poster doesn't mind that I am jumping onto his thread, but since we already are on the topic of the relationship between speed, frequency and wavelength of light, perhaps somebody could clarify this question for me:

(Berkeley Review, Physics Section 10, Pass. II, #14): What is true of different colors of light in a medium?

I picked (c): As speed decreases, wavelength decreases. The correct answer, however, was (d): As frequency increases, the wavelength decreases.

I understand the relationship v = wavelength x frequency, where v = c/n. However, I don't see why (c) is incorrect, since as light moves from a vacuum to a material medium, the velocity (and wavelength) decrease while frequency stays the same. Am I to assume that this would have been the correct answer if the question was asking about the change a monochromatic wave of light would experience as it moved into a different medium?

Any clarification is very much appreciated!

 

[whiteshadodw]

I hope the original poster doesn't mind that I am jumping onto his thread, but since we already are on the topic of the relationship between speed, frequency and wavelength of light, perhaps somebody could clarify this question for me:

(Berkeley Review, Physics Section 10, Pass. II, #14): What is true of different colors of light in a medium?

I picked (c): As speed decreases, wavelength decreases. The correct answer, however, was (d): As frequency increases, the wavelength decreases.

I understand the relationship v = wavelength x frequency, where v = c/n. However, I don't see why (c) is incorrect, since as light moves from a vacuum to a material medium, the velocity (and wavelength) decrease while frequency stays the same. Am I to assume that this would have been the correct answer if the question was asking about the change a monochromatic wave of light would experience as it moved into a different medium?

Any clarification is very much appreciated!

v (wave speed in units length/time) = f (1/sec) * wavelength (m) = m/s

in a given medium, the speed of any EM radiation is constant pretty much (except some wavelengths have different indices of refraction in a given medium, this is the principle of dispersion). since wave velocity/speed is constant, then as you change frequency wavelength has to change. we can look at it another way

v/wavelength = frequency ; but v is a constant so we can replace it with a k or i like 1 since we don't need to focus on it:

1/wavelength = frequency

we can see that wavelength is inversely proportional to frequency. thus, if frequency gets larger wavelength HAS to get smaller.

 

[MD Odyssey]

It seems as if there is a lot of mixing between true wave phenomenon like water or sound and light, which is a fundamentally different thing because light really isn't a wave. In my experience, a lot of students like to talk about wave-particle duality, but they don't really understand what they're saying. Light will make a lot more sense when abandon the facade of it being a wave.

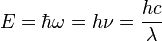
There are several questions being asked, so I'm going to try and answer each one concisely. Let me first give a couple of fundamental relationships:

1) The energy of a photon is proportional to its frequency and inversely proportional to its wavelength. That's the law.

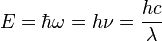
2) The index of refraction of a particular material is given by

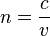
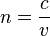
where c is the speed of light in a vacuum (constant) and v is the velocity of light through the medium of interest. In general, these are not the same because light doesn't travel a straight path through a material. It gets absorbed, re-emitted, absorbed, re-emitted, and so on as it propagates through the material and the re-emission occurs in random directions. Therefore, it takes longer for light to travel through something like glass or water because it travels a greater distance, not because it travels slower.

3) An earlier commenter stated that

The frequency hasn't changed, but the wavelength has, and hence the refraction.

This is completely incorrect. Frequency and wavelength describe the same phenomenon. The index of refraction is different for different materials because photons travel a longer path in media such as glass or water than they do in a vacuum.

4) The discussion of Doppler effect for waves in media like water or air is fundamentally different that that of light. Consider the physical phenomenon - water and sound waves have a medium through which they propagate through, but light doesn't! A discussion of the Doppler effect for electromagnetic waves is considerably more difficult - that's what special relativity is all about.

5) For classical particles, such as a bullet, the energy is proportional to the square of the velocity. Energy of a photon is defined completely different, as several posters have tried to point out. It's actually much deeper than that. Photons don't have energy - they are energy. Their energy, frequency, and wavelength are all fixed the moment that the photon is created. Think of them as little packets of energy - they carry spin, momentum, energy, but no mass. They are the quantization of the electromagnetic field and they only exist at the speed of light. Furthermore, regardless of your reference frame, they will always be traveling at the speed of light, c.

I read through the comments in this thread and there are a lot of inaccurate statements, so please take some time to read through what I've written and if any of it doesn't make sense, feel free to ask.

Also, the Wikipedia entry on the Doppler effect is very good, but just make sure that you don't apply it to light - there is a Doppler shift for EM radiation, but it is fundamentally different than that for sound or water waves.
​

 

[Labminion]

Thank you both for your replies.

Whiteshadow - I suppose my next question is, since the question is referring to different wavelengths of colored light, they necessarily do not have the same speed in a material medium (for n = c/v to hold true). In this instance, we cannot really equate the product of wavelength x frequency for different wavelengths, since their velocities in the medium are all different. Am I still misunderstanding this? Or perhaps, the difference in their velocities is small enough that we may ignore it and set them equal to each other anyway?

MD Odyssey - I am wondering if some of the misunderstanding some of us (i.e., me!) are experiencing is due to the explanations we are reading in our review material. Both my Princeton Review book and my Berkeley Review book claim that as light enters a new medium, it speed changes, but its frequency does not. (From my Princeton Review book: "When a wave passes into another medium it's speed changes, but its frequency does not. Because f is constant, [this rule] tells us that the wavelength is proportional to wave speed."). Perhaps this is an oversimplification that the review books are teaching us (i.e. the average velocity of the wave is slower because it travels a longer distance, though in actuality the instantaneous velocity remains the same)? What you are saying makes sense to me, but is a bit different than what I have been reading. I'll have to think on it some more.

Thanks again to you both for your input.

 

[Labminion]

It seems the Berkeley Review book is contradicting itself in its explanation of the relationship between frequency/wavelength/wave speed. In the text (pg. 244) it says, "Electromagnetic waves of different wavelengths travel at different speeds through material substances (i.e., anything other than a vacuum)." Later, in an answer explanation (#30), it says, "Light traveling through a medium will exhibit the same wave speed regardless of the frequency." This seems to support what you were saying earlier, MD Odyssey. Nevertheless, these two explanations seem contradictory to me.

 

[MT Headed]

What is true of different colors of light in a medium?

I picked (c): As speed decreases, wavelength decreases.

While MDOdyssey is obviously more qualified than most of us to speak on the topic, I thought you might appreciate the MCAT approach to this problem

Lab, your answer would be correct if they were asking about the phenomenon of light making the transition from one medium to another. In that case, frequency is a constant, so speed and wavelength will change as needed.

However, examine the question stem closely. The question is asking about different kinds of light that are already in a medium. The medium isn't changing in your question stem. Therefore the speed is going to be (nearly) a constant. Yes, as your book points out, the speeds are slightly different for different frequencies, but the difference is small and not relevant to this problem. Since speed is a constant, it's the other two variables (wavelength and frequency) that will adjust to accommodate your scenario.

MCAT practice questions are notorious for taking a couple of related phenomena taught closely together (i.e. different frequencies in same medium vs. same frequency in different media) and trying to determine who was paying attention in class that day.

 

[Labminion]

Ahh, this makes sense. Thank you for the explanation, MT. I wasn't sure if the differences in velocities between different wavelengths of light could be regarded as negligible (outside of the context of dispersion, of course). I shall have to be more careful going forward about making sure I am answering the real question being asked.

 

[MD Odyssey]

Ahh, this makes sense. Thank you for the explanation, MT. I wasn't sure if the differences in velocities between different wavelengths of light could be regarded as negligible (outside of the context of dispersion, of course). I shall have to be more careful going forward about making sure I am answering the real question being asked.

This business about the speed of light changing really bothers me because it isn't true. The speed of light is a constant in all reference frames. The velocity changes as light enters into a medium because it doesn't travel a straight line through the material. This phenomenon is what gives rise to the index of refraction. It's also what leads to dispersion, since the index of refraction is actually a function of frequency - this is a second-order effect which is not usually taught in introductory physics courses, but explains how prisms work.

What's really going on here is that the velocity that light travels in a medium is actually dependent upon its energy (or frequency, or wavelength - all three terms are describing the same quantity), therefore the index of refraction is dependent upon the energy as well.

I want to also point out that the BR use of wave velocity is imprecise and dangerous - they could be referring to the phase velocity or the group velocity, which are not the same, in general. So, don't get too caught up on the terminology.

Here's what I would know for the MCAT:

1. Don't think of light as a wave - think of it as a shower of particles called photons that all carry energy, spin, and momentum.
2. The energy of a photon is given by the equation I cited earlier.
3. Wavelength, frequency, and angular frequency are all measuring the same fundamental thing, energy, thus they are not independent quantities in any way.
4. The speed of light is a constant in all reference frames.
5. The path that light travels in a medium depends upon the material as well as the energy of the photon.
6. The index of refraction for a medium is given as the ratio of the speed of light (constant) to the velocity of light in that medium
7. Because of #5, the index of refraction for a medium will depend upon the frequency of the light

I think if you understand these things, you'll be set.

I realize that thinking of light as a bunch of particles runs counter to what they tell you in physics class. This is because physics teachers love to talk about wave-particle duality, but they almost always do a bad job of explaining what that means. The one place thinking of light as a wave makes sense is when working diffraction or interference problems. For most people, description of these phenomena using the wave model of light is more intuitive - a particle model can be made, but it's a lot less intuitive.

 

[Labminion]

Wow, MD Odyssey, your knowledge of this material is truly impressive. I am a little bit in awe of you. 🙂 Thanks for taking the time to break it down for me.

I am going to re-attempt all the EM/light/wave questions that I did a couple of days ago with this new perspective, and see if I can answer them correctly. I was making a lot of mistakes (on what I previously thought was very straightforward material), so there was obviously a fundamental lack of understanding on my part. Thanks again for your help.

 

[Eliyah]

This business about the speed of light changing really bothers me because it isn't true. The speed of light is a constant in all reference frames. The velocity changes as light enters into a medium because it doesn't travel a straight line through the material. This phenomenon is what gives rise to the index of refraction. It's also what leads to dispersion, since the index of refraction is actually a function of frequency - this is a second-order effect which is not usually taught in introductory physics courses, but explains how prisms work.

What's really going on here is that the velocity that light travels in a medium is actually dependent upon its energy (or frequency, or wavelength - all three terms are describing the same quantity), therefore the index of refraction is dependent upon the energy as well.

I want to also point out that the BR use of wave velocity is imprecise and dangerous - they could be referring to the phase velocity or the group velocity, which are not the same, in general. So, don't get too caught up on the terminology.

Here's what I would know for the MCAT:

1. Don't think of light as a wave - think of it as a shower of particles called photons that all carry energy, spin, and momentum.
2. The energy of a photon is given by the equation I cited earlier.
3. Wavelength, frequency, and angular frequency are all measuring the same fundamental thing, energy, thus they are not independent quantities in any way.
4. The speed of light is a constant in all reference frames.
5. The path that light travels in a medium depends upon the material as well as the energy of the photon.
6. The index of refraction for a medium is given as the ratio of the speed of light (constant) to the velocity of light in that medium
7. Because of #5, the index of refraction for a medium will depend upon the frequency of the light

I think if you understand these things, you'll be set.

I realize that thinking of light as a bunch of particles runs counter to what they tell you in physics class. This is because physics teachers love to talk about wave-particle duality, but they almost always do a bad job of explaining what that means. The one place thinking of light as a wave makes sense is when working diffraction or interference problems. For most people, description of these phenomena using the wave model of light is more intuitive - a particle model can be made, but it's a lot less intuitive.

This is the best explanation by far i have read in Physics ...Thank you sir
But my concept is at some places still blurry . Can you explain what you meant by "Index of Refraction is a function of frequency".
Secondly as photons have fixed speed we say light has a constant speed too (as it's made of photons) . Right?