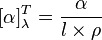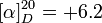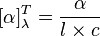Optical Rotation TBR

[BradyC]

Hi. I am reviewing a question from the end of chapter 25 set in the first TBR orgo I book in Chapter 3. The question is #8. I don't understand the explanation of "when using a polarimeter, an observed optical rotation of +233 and -127 would result in the same reading (given that a full circle is 360 degrees)". How can the observed rotation be the same if the specific activities are different? Thanks.

---

Members don't see this ad.

 

[Czarcasm]

Can you post the relevant question and additional information? It's really hard to help without that info.

 

[Czarcasm]

I'm glad you posted this because you made me realize something I otherwise wouldn't have noticed.

I looked into this and came across this Wikipedia posting that might help clear things up:

Dealing with large and small rotations
If a compound has a very large specific rotation or a sample is very concentrated, the actual rotation of the sample may be larger than 180°, and so a single polarimeter measurement cannot detect when this has happened (for example, the values +270° and −90° are not distinguishable, nor are the values 361° and 1°). In these cases, measuring the rotation at several different concentrations allows one to determine the true value. Another method would be to use shorter path-lengths to perform the measurements.

In cases of very small or very large angles, one can also use the variation of specific rotation with wavelength to facilitate measurement. Switching wavelength is particularly useful when the angle is small. Many polarimeters are equipped with a mercury lamp (in addition to the sodium lamp) for this purpose.

To understand why altering the concentration or path-length might result in different degrees of rotations:

For pure liquids
This equation is used:

In this equation, α (Greek letter "alpha") is the measured rotation in degrees, l is the path length in decimeters, and ρ (Greek letter "rho") is the density of the liquid in g/mL, for a sample at a temperature T (given in degrees Celsius) and wavelength λ (in nanometers). If the wavelength of the light used is 589 nanometers (the sodium D line), the symbol “D” is used. The sign of the rotation (+ or −) is always given.

For solutions
A different equation is used:

In this equation, α (Greek letter "alpha") is the measured rotation in degrees, l is the path length in decimeters and c is the concentration in g/mL, for a sample at a temperature T (given in degrees Celsius) and wavelength λ (in nanometers).[1] If the wavelength of the light used is 589nanometer (the sodium D line), the symbol “D” is used. The sign of the rotation (+ or −) is always given. When using this equation, the concentration and the solvent may be provided in parentheses after the rotation. The rotation is reported using degrees, and no units of concentration are given (it is assumed to be g/100mL).

For example:

Obviously though, there's a big difference here in terms of specific rotation (which is the value reported by certain conventions: 1 decimeter and a sample concentration of 1 g/mL) and non-standard optical rotation (which can be altered as mentioned above). In other words, by changing the recommended concentration or density, you would no longer consider it a specific degree of rotation but instead a unique optical rotation value at those distinct conditions.

I hope that makes sense