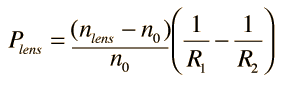thin lens equation and lensmaker equation

[dudewheresmymd]

do we even need to know the sign conventions for 1/f=1/do+1/di if we just use the 5 case converging and SUV for diverging from TBR?

If so, can someone clarify how to determine positive or negative for do and di?

I know for f (+) converging and f (-) diverging lens.

I've just been using the 5 cases thing from TBR and have been getting most questions right...But I tend not to use the lensmaker equation as it mixes me up, but I'm concerned we may get a question that you need to find the exact distance of the image or something, and I may get this wrong if I don't have the sign conventions down.


2nd) would we have to have the lensmaker equation memorized? If we put a converging or diverging lens under water (n=1.33) or oil (not sure what the n is), does the focal length increase or decrease? I didn't really have good practice with this in physics so somewhat confused.


Thanks!

---

Members don't see this ad.

 

[Maxxxx]

For me, memorizing the lens equation is SOOOO much easier than trying to memorize each case separately. The equation is simple and always works,

1/f = 1/0 + 1/i

1) object (o) is always +
2) For mirrors, images (i) and focal points (f) are always + when they are on the same side of o. (just think: mirrors reflect)
3) For lenses, i and f are always + when they are on the other side of o. (think: you see THROUGH the lens)
4) +i means image is real and inverted.

I think these "rules" are very straight forward. There's no need to memorize any exceptions (like object closer/further than focal length).

For example, take a divergent lens. o is +. Since f is on the same side of o, f has to be - (you see THROUGH a lens). Plug in the equation, you'll find 1/f is - and 1/0 is +, and i has to be - no matter what values of o or f.

Edit: I'm also very interested in your 2nd question.

 

[milski]

Maxxx already answered most of what you need to know. Considering that you will get different answers, depending on whether you use +/-, obviously you need to use the correct sign to get the correct answer. The rules above would help you do that. I am a very much a math person - I'd rather use the numbers in a formula and make sense of the result vs. trying to memorize a list of possible combinations. But that's just me - if you're more comfortable using TBR's cases, go with that.

Also, this is the lens equation, not the lensmaker's equation. I think TBR has it mislabled. The lensmaker's equation relates the physical dimensions of the lens, the refractive index of its material and the media and its focal length. I'm not sure if TBR has it but wikipedia has the version for air: http://en.wikipedia.org/wiki/Lens_(optics)#Lensmaker.27s_equation For general medial, you want to replace the 1 in (n-1) with the refraction index of the media. In the boundary case where n1=n2 you'll get that P=1/f=0 and the focal length is infinity, which makes sense since there will be no refraction at all in this case.

 

[dudewheresmymd]

For me, memorizing the lens equation is SOOOO much easier than trying to memorize each case separately. The equation is simple and always works,

1/f = 1/0 + 1/i

1) object (o) is always +
2) For mirrors, images (i) and focal points (f) are always + when they are on the same side of o. (just think: mirrors reflect)
3) For lenses, i and f are always + when they are on the other side of o. (think: you see THROUGH the lens)
4) +i means image is real and inverted.

I think these "rules" are very straight forward. There's no need to memorize any exceptions (like object closer/further than focal length).

For example, take a divergent lens. o is +. Since f is on the same side of o, f has to be - (you see THROUGH a lens). Plug in the equation, you'll find 1/f is - and 1/0 is +, and i has to be - no matter what values of o or f.

Edit: I'm also very interested in your 2nd question.

Thanks! Hmm, what do you mean by since f is on same side of o? doesn't a divergant lens have focal lengths on both sides? Still a bit confused? Do you have another example we can do?

Maxxx already answered most of what you need to know. Considering that you will get different answers, depending on whether you use +/-, obviously you need to use the correct sign to get the correct answer. The rules above would help you do that. I am a very much a math person - I'd rather use the numbers in a formula and make sense of the result vs. trying to memorize a list of possible combinations. But that's just me - if you're more comfortable using TBR's cases, go with that.

Also, this is the lens equation, not the lensmaker's equation. I think TBR has it mislabled. The lensmaker's equation relates the physical dimensions of the lens, the refractive index of its material and the media and its focal length. I'm not sure if TBR has it but wikipedia has the version for air: http://en.wikipedia.org/wiki/Lens_(optics)#Lensmaker.27s_equation For general medial, you want to replace the 1 in (n-1) with the refraction index of the media. In the boundary case where n1=n2 you'll get that P=1/f=0 and the focal length is infinity, which makes sense since there will be no refraction at all in this case.

yup i realized they have it mislabeled.

http://hyperphysics.phy-astr.gsu.edu/hbase/geoopt/lenmak.html

it says power diminishes in any other media than air, i'm guessing they mean focal length increases then..but does this apply for both converging and diverging lenses (1/r1-1/r2) would be constant, and if "n sub 0" new medium index increases then power of the lens has to decrease and therefore focal length has to increase? can you guys verify my math/reasoning?

Lastly, would this work for both converging/diverging?

Thanks!! 🙂

 

[Maxxxx]

Thanks! Hmm, what do you mean by since f is on same side of o? doesn't a divergant lens have focal lengths on both sides? Still a bit confused? Do you have another example we can do?

With lenses just look at the the half that's closer to o. So I would draw divergent lens the same way as I would a concave mirror (just imaging parallel lines hitting the lens then scatter outwardly). Then it's more clear that f is on the same side of o.

Another example! Let's do convergent lens then.
Per above, o = +, f = +. Plug into equation, 1/f = 1/o + 1/i, and 1/i = 1/f - 1/o
now, if o <f , then 1/f < 1/o; and 1/i has to be -; image is upright and virtual
if o >f, then 1/f > 1/o; and 1/i is +; image is real and inverted.

 

[milski]

http://hyperphysics.phy-astr.gsu.edu/hbase/geoopt/lenmak.html

it says power diminishes in any other media than air, i'm guessing they mean focal length increases then..but does this apply for both converging and diverging lenses (1/r1-1/r2) would be constant, and if "n sub 0" new medium index increases then power of the lens has to decrease and therefore focal length has to increase? can you guys verify my math/reasoning?

Lastly, would this work for both converging/diverging?

Thanks!! 🙂

Yes, this is all correct. As n0 gets closer to nlens, the power diminishes and the focal length increases. In the opposite case, as the difference between them increases, the power of the lens increases and the focal distance decreases.

There are lenses on the market nowadays, made from materials with higher nlens than typical glass. That allows for making a thinner lenses with the same power, which in turn supposedly look better. 😉

 

[dudewheresmymd]

Yes, this is all correct. As n0 gets closer to nlens, the power diminishes and the focal length increases. In the opposite case, as the difference between them increases, the power of the lens increases and the focal distance decreases.

There are lenses on the market nowadays, made from materials with higher nlens than typical glass. That allows for making a thinner lenses with the same power, which in turn supposedly look better. 😉

ah hah! thanks 🙂 good ol' milski physics major to the rescue.

 

[dudewheresmymd]

For me, memorizing the lens equation is SOOOO much easier than trying to memorize each case separately. The equation is simple and always works,

1/f = 1/0 + 1/i

1) object (o) is always +
2) For mirrors, images (i) and focal points (f) are always + when they are on the same side of o. (just think: mirrors reflect)
3) For lenses, i and f are always + when they are on the other side of o. (think: you see THROUGH the lens)
4) +i means image is real and inverted.

I think these "rules" are very straight forward. There's no need to memorize any exceptions (like object closer/further than focal length).

For example, take a divergent lens. o is +. Since f is on the same side of o, f has to be - (you see THROUGH a lens). Plug in the equation, you'll find 1/f is - and 1/0 is +, and i has to be - no matter what values of o or f.

Edit: I'm also very interested in your 2nd question.

Quick follow up-- TBR says if object is to left of lens d(o) is positive. if object is to right of lens, this value is (-). when would the object ever be to the right of a lens?