Work done by Gravity

[5words]

So i am having problem understanding the reasoning behind this question:


upload image

I understand why D is the best answer, however, i dont get the reasoning behind C , i have highlighted the answer choice:

upload image

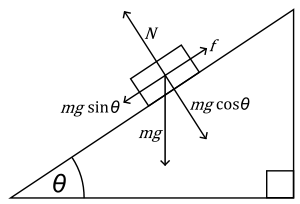
Now there is two formula for the work done by Gravity, the First is mg(delta)h and the second is mgsin(Theta)d (or is it not)? because the vertical component of gravity does no work. Using, any of those formula , by deflating the pad.. delta h is changing so why is W by grav not changing? Same with mgsing(theta) as you deflate the pad it;s changing as well.. So, why are they saying work done by Grav wont change even if Theta (indirectly h) are changing.

Thanks

@aldol16 @MedVIP @Pono_0001 @NextStepTutor_3 @neurodoc

---

Members don't see this ad.

 

[aldol16]

Now there is two formula for the work done by Gravity, the First is mg(delta)h and the second is mgsin(Theta)d (or is it not)? because the vertical component of gravity does no work. Using, any of those formula , by deflating the pad.. delta h is changing so why is W by grav not changing? Same with mgsing(theta) as you deflate the pad it;s changing as well.. So, why are they saying work done by Grav wont change even if Theta (indirectly h) are changing.

Think about what that delta h or d means. It means that gravity is exerting a force on an object that moves some displacement. Here, that displacement is fixed - from the top of the ramp to the bottom. The d is the same - it's going to move the same distance in the frame of reference of the ramp.

 

[5words]

Think about what that delta h or d means. It means that gravity is exerting a force on an object that moves some displacement. Here, that displacement is fixed - from the top of the ramp to the bottom. The d is the same - it's going to move the same distance in the frame of reference of the ramp.

So which formula is the best in this case.. Indeed i do see why delta h and even d wont change. So, shouldnt i use the second formula to compute W by grav?

 

[FCMike11]

It's amazing I made what I did on the physical sciences section on the MCAT. Almost a year out from taking the exam and most of that information is gone.


Sent from my Nexus 6P using SDN mobile

 

[5words]

It's amazing I made what I did on the physical sciences section on the MCAT. Almost a year out from taking the exam and most of that information is gone.


Sent from my Nexus 6P using SDN mobile

yeah, it doesnt stay for long .. Got A in Phys I , II even Took Cal III

 

[aldol16]

So which formula is the best in this case.. Indeed i do see why delta h and even d wont change. So, shouldnt i use the second formula to compute W by grav?

The formulas you have are the exact same - they two versions of the same formula. The key thing to note is that you want the force exerted in the direction of the displacement. The displacement is along the direction of the ramp. Therefore, you want the component of gravity that acts in the direction of the ramp, which is mgsin(theta). The first formula, mg*delta h, is applicable only when the full force of gravity, mg, is exerted in the direction of displacement, delta h - this isn't the case here.

 

[5words]

the full force of gravity, mg, is exerted in the direction of displacement, delta h - this isn't the case here.

Hence my question, because theta is changing as the pad is getting deflated; thus mgsintheta changes as well.. So why are they saying it shouldn't change? w= F x d .. d doesn't change but F x does. So am i missing something?

 

[aldol16]

Hence my question, because theta is changing as the pad is getting deflated; thus mgsintheta changes as well.. So why are they saying it shouldn't change? w= F x d .. d doesn't change but F x does. So am i missing something?

Ah yes, I believe you are right. The work should change because the angle is changing.

 

[5words]

Ah yes, I believe you are right. The work should change because the angle is changing.

So are they wrong then? cause it seems as if they are only relying on the following formula : W = mgh .. And gravity is a conservative force, so the work should depend on the path taken. Since they both start at hmax or theta max and end at 0, the work ought to stay the same , however , i cant conceptually arrive to that point by using mgsin(theta)d .. ill keep on thinking about this..

 

[aldol16]

So are they wrong then? cause it seems as if they are only relying on the following formula : W = mgh .. And gravity is a conservative force, so the work should depend on the path taken. Since they both start at hmax or theta max and end at 0, the work ought to stay the same , however , i cant conceptually arrive to that point by using mgsin(theta)d .. ill keep on thinking about this..

Sorry, it's my mistake. I got lost in the variables. Here's your mistake. The force of gravity always points directly down. Draw the free body diagram. And the definition of work done is the force multiplied by the displacement that is in the direction of that force. Therefore, since the force is gravity and it points down, the displacement of the box in the direction of that force is only the vertical distance, or height. This remains the same regardless of whether the angle changes during movement.

The force that does work in the x-direction is actually the normal force. If you draw a free body diagram, you should clearly see this. The normal force pushes up on the box at an angle and produces displacement in the x-direction. One way to conceptualize this is to compare dropping an object from height h and letting it roll down an incline from height h. In the first scenario, it's just falling straight down. The addition of an incline is what causes the horizontal motion so it must be the incline that's doing the work in the x-direction.

 

[Pono_0001]

correct me if I'm wrong. yes d is the same but since the force that drives the box down depends on the angle, and as the angle is decreasing the F is decreasing too. a fixed d with a decreasing f you have less work done. another way to think about decreasing f is via acceleration from f=ma. you can visualize how by lowering the slope, the object on the slope is accelerate less, hence a smaller f.

 

[aldol16]

correct me if I'm wrong. yes d is the same but since the force that drives the box down depends on the angle, and as the angle is decreasing the F is decreasing too. a fixed d with a decreasing f you have less work done. another way to think about decreasing f is via acceleration from f=ma. you can visualize how by lowering the slope, the object on the slope is accelerate less, hence a smaller f.

You're talking about work in the x-direction which is not work done by gravity but rather work done by the normal force.

 

[Pono_0001]

work in the x direction would be along the incline. work done by normal is normal to the direction of motion, since there's no motion perpendicular to the incline, and work = displacement x force, work done by normal would be zero. this is the same as calculating work done on a box when you pull it with a string at an angle.
/
here's a link on this discussion from another forum if it's not clear:
Work done by gravity on a object on an inclined plane

gravitional force is what drives the motion, it's just that the displacement is at an angle with the direction of the gravitational force, so you use cross product here. it's still work done by gravity.

 

[aldol16]

work in the x direction would be along the incline. work done by normal is normal to the direction of motion, since there's no motion perpendicular to the incline, and work = displacement x force, work done by normal would be zero. this is the same as calculating work done on a box when you pull it with a string at an angle.
/
here's a link on this discussion from another forum if it's not clear:
Work done by gravity on a object on an inclined plane

gravitional force is what drives the motion, it's just that the displacement is at an angle with the direction of the gravitational force, so you use cross product here. it's still work done by gravity.

You're talking about a coordinate system with a horizontal defined by the inclined plane. I'm talking about a coordinate system with a horizontal being defined by the true horizontal, meaning that the inclined plane would be at an angle to the horizontal x-axis. But to make things easier to see using your argument, let's switch to your coordinate system.

The work done by gravity is still the same here. So let's draw the free body diagram like so:

You've defined the x-axis as the incline. That's fine. But the force of gravity is at an angle to that of the x-axis. The force of gravity is always exerted straight down towards the center of the Earth, as drawn. The magnitude does not change - it's always m*g pointing straight downwards to the center of the Earth, no matter how you define your coordinate system. As you can see in this picture, the net displacement in the direction of the force of gravity is simply the height of the incline. You can repeat this exercise with any incline you want (any theta where 0 < theta < pi/2) and you will get the same result if the box always starts at the same height. Therefore, the work done by gravity does not change no matter the slope. Does that make sense now? Defining your coordinate system with the x-axis along the incline actually complicates the problem in this case because it's asking specifically by the work done by gravity, which is a force that acts strictly in the vertical direction (in the coordinate system where the x-axis is the true horizontal and the y-axis is the vertical).

This then begs the (related) question of how you get horizontal displacement at all then (where horizontal is the true horizontal). Well, remember Newton's third law. The object is pressing down on the plane and the plane is pressing right back on the object. So immediately, as drawn in the picture, you can see that the normal force provides the impetus for displacement in the horizontal direction (true horizontal).

 

[5words]

You're talking about a coordinate system with a horizontal defined by the inclined plane. I'm talking about a coordinate system with a horizontal being defined by the true horizontal, meaning that the inclined plane would be at an angle to the horizontal x-axis. But to make things easier to see using your argument, let's switch to your coordinate system.

The work done by gravity is still the same here. So let's draw the free body diagram like so:

You've defined the x-axis as the incline. That's fine. But the force of gravity is at an angle to that of the x-axis. The force of gravity is always exerted straight down towards the center of the Earth, as drawn. The magnitude does not change - it's always m*g pointing straight downwards to the center of the Earth, no matter how you define your coordinate system. As you can see in this picture, the net displacement in the direction of the force of gravity is simply the height of the incline. You can repeat this exercise with any incline you want (any theta where 0 < theta < pi/2) and you will get the same result if the box always starts at the same height. Therefore, the work done by gravity does not change no matter the slope. Does that make sense now? Defining your coordinate system with the x-axis along the incline actually complicates the problem in this case because it's asking specifically by the work done by gravity, which is a force that acts strictly in the vertical direction (in the coordinate system where the x-axis is the true horizontal and the y-axis is the vertical).

This then begs the (related) question of how you get horizontal displacement at all then (where horizontal is the true horizontal). Well, remember Newton's third law. The object is pressing down on the plane and the plane is pressing right back on the object. So immediately, as drawn in the picture, you can see that the normal force provides the impetus for displacement in the horizontal direction (true horizontal).

Now that you figured it out... Do you understand my first question now? (The normal force indeed does no work because it;s perpendicular to the plane) In the incline plane you incline your axis , whereas in the Banked curve , you incline the plane. (so the normal force does work in the banked curve only, or etc..)

Anyways, so is W = mgsintheta times d a viable formula? If it is then, the EK AC is wrong when it says that the work remain static, The F could still stay static because F is a vector, thus F by grav can also be equal to = sqrt( Fx ^2 + Fy^2), thus changing the angle wont necessary change the value of F by grav , since as theta change Fx decrease by the same amount that Fy is increasing. Hence the dilemma , if you supposed to W by grav = mgsin(theta) d , here because only the Fx component of grav does Work the formula W by grav = mgsintheta times d becomes wrong. That's the dilemma. So idk if i shold stick to W = mgh or W= Fsing theta .. because work down by gravity is a conservative force. Or are there scenario where the aforementioned formula could work, such as Work done by the Horizontal component of gravity but not necessarily gravity.

 

[aldol16]

Now that you figured it out... Do you understand my first question now? (The normal force indeed does no work because it;s perpendicular to the plane) In the incline plane you incline your axis , whereas in the Banked curve , you incline the plane. (so the normal force does work in the banked curve only, or etc..)

Anyways, so is W = mgsintheta times d a viable formula? If it is then, the EK AC is wrong when it says that the work remain static, The F could still stay static because F is a vector, thus F by grav can also be equal to = sqrt( Fx ^2 + Fy^2), thus changing the angle wont necessary change the value of F by grav , since as theta change Fx decrease by the same amount that Fy is increasing. Hence the dilemma , if you supposed to W by grav = mgsin(theta) d , here because only the Fx component of grav does Work the formula W by grav = mgsintheta times d becomes wrong. That's the dilemma. So idk if i shold stick to W = mgh or W= Fsing theta .. because work down by gravity is a conservative force. Or are there scenario where the aforementioned formula could work, such as Work done by the Horizontal component of gravity but not necessarily gravity.

Go back to the original derivations of these equations. Let's refer back to the free-body diagram:

As you can see, the reason why W = m*g*sin(theta) applies is because work is force multiplied by the displacement in the direction of the force. So let's use your frame of reference here - let's set the x-direction to be the plane of the inclined plane. That makes the W = F*d = m*g*sin(theta)*d. Here's where you're missing the crucial step. What's d? d here is the length of the hypotenuse of the ramp. Do we agree there? As long as d is the hypotenuse of the ramp, then it must also be necessary that d = h/sin(theta). Make sure you see this. So substitute back in for the work formula: W = m*g*sin(theta)*d = m*g*sin(theta)*h/sin(theta) = m*g*h.

 

[5words]

Go back to the original derivations of these equations. Let's refer back to the free-body diagram:

As you can see, the reason why W = m*g*sin(theta) applies is because work is force multiplied by the displacement in the direction of the force. So let's use your frame of reference here - let's set the x-direction to be the plane of the inclined plane. That makes the W = F*d = m*g*sin(theta)*d. Here's where you're missing the crucial step. What's d? d here is the length of the hypotenuse of the ramp. Do we agree there? As long as d is the hypotenuse of the ramp, then it must also be necessary that d = h/sin(theta). Make sure you see this. So substitute back in for the work formula: W = m*g*sin(theta)*d = m*g*sin(theta)*h/sin(theta) = m*g*h.

OMG!!! INSNAE!!! DUDE UR THE BEST!!!

EDIT: You know what i actually have another question, which has been bothering def posting it tomorow