AAMC FL C/P 58 explanation

[Future_Bone_Docta]

---

Members don't see this ad.

A tall tube is evacuated, and its stopcock closed. The open end of the tube is immersed into a container of water (density 103 kg/m3) that is open to the atmosphere (pressure 105 N/m2).

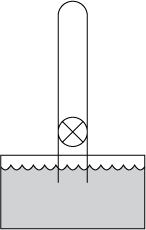
When the stopcock is opened, how far up the tube will the water rise?

• A. 1 m
• B. 5 m
• C. 10 m
• D. 20 m

So I got the question right, and I thought my logic was sound, the AAMC kinda had me second guessing my logic though, and I was wondering if someone could confirm whether it sounds conceptually sound. The AAMC basically said "P= (p)(g)(h). Okay.

My logic was that I manipulated Bernoulli's equation:

P + pgh + 1/2pv^2 = P + pgh + 1/2pv^2

1) we are dealing with stationary fluids. hence no kinetic energy. So we get:

P + pgh = P + pgh

The fluid in the "bowl" technically has a height of 0 relative to the tube, so we can take "pgh" out of one half:

P + pgh= P

Technically the pressure in a "vacuumed" evacuated tube is negligible, so assume 0... giving us

P= (p)(g)(h)

Hope I can get some verification from some of you physics gurus out there whether or not my logic was sound or I just got lucky, Thanks!

 

[BerkReviewTeach]

Before you solve this, you should check your density of water that you listed. It is probably 1003 kg/m^3.

You in essence derived the gauge pressure equation. That is exactly the formula necessary to get this right. Atmospheric pressure is about 1 Bar, which is 100,000 Pa. The gauge pressure of the water in the tall column must be 100,000 Pa.

100,000 = (rho)gh = 1003 x 10 x h = 10,030 h

100,000/10,030 = h

10 = h

But there is a WAYYYYYYYY easier solution to this question that we highly recommend. If you are familiar with scuba diving, you learn that every ten meters (around 32 feet) deeper you go down water, you experience a gain of 1 atmosphere of pressure. So 1 atm = 10 m of water, choice C.