- Joined
- Feb 12, 2011
- Messages
- 522
- Reaction score
- 2
cause destructive/construcive interference?
So, they have to have the same frequency for constructive/destructive interference to occur, right?

The perfect example of this is the signal received by an AM radio:

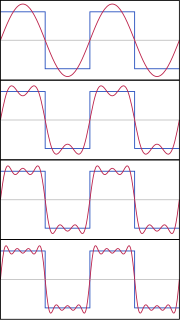
Notice that there are two waves which obviously have different frequencies that are superimposed to form the AM modulated signal on the bottom. It can be proven, with a lot of calculus, that any periodic function can be written as a sum of sines and cosines, each with a different frequency. This is the basic idea of something known as Fourier analysis. Here is a more complicated example of some sines and cosines added together to produce what looks like a square wave. You can imagine that, given an infinite number of sines and cosines, eventually you'll reproduce the original wave.

AAMC #7 SPOILER, DON'T READ IF YOU HAVEN'T TAKEN IT
this is almost exactly what my question came from actually. The question asked, how come cell phones can recieve and transmit signals (a phone call) both at hte same time. and the answer said that because they're at different frequencies, they don't interfere with one another....care to shed light on this? I'm not sure if I fully understand based on what the above responses have been. I thought of beats too, that's why I eliminated that answer.
If two frequencies are far enough apart, there won't be superposition for interference. The limit is about 15 Hz, so if two sound waves are separated by more than 15 Hz, you will hear two different tones (no beats).
