- Joined
- Jan 12, 2015
- Messages
- 23
- Reaction score
- 3
- Points
- 4,551
- Pre-Dental
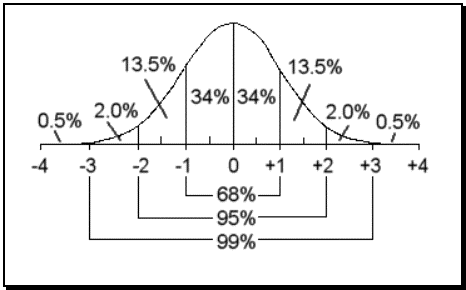
Assume that the scores on an entrance exam to collegeville are normally distributed with a mean of 70 and a standard deviation of 8. To earn a scholarship a student's score needs to be on the top 2.5%. What is the minimum score that will guarantee a scholarship?
The answer is 86
The solution says: To be the top 2.5% the score should be 2 standard deviations above the mean. 70+8+8=86
I never took statistics, and I don't understand the solution. Can somebody explain this to me?
Thank you.
The answer is 86
The solution says: To be the top 2.5% the score should be 2 standard deviations above the mean. 70+8+8=86
I never took statistics, and I don't understand the solution. Can somebody explain this to me?
Thank you.