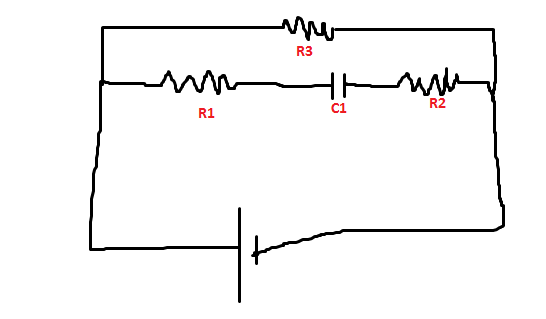
An uncharged capacitor is added to a circuit as follows:

S4 and S3 are then closed, causing the capacitor to be charged. Which of the following statements is correct?
A.The maximum charge stored in the capacitor would be the same if S3 had remained open.
B. The capacitor would not be charged if S3 had remained open.
C.The maximum charge stored in the capacitor would be lower if S3 had remained open.
D. The maximum charge stored in the capacitor would be higher if S3 had remained open.
Answer: D. UUUUUUmmm???

S4 and S3 are then closed, causing the capacitor to be charged. Which of the following statements is correct?
A.The maximum charge stored in the capacitor would be the same if S3 had remained open.
B. The capacitor would not be charged if S3 had remained open.
C.The maximum charge stored in the capacitor would be lower if S3 had remained open.
D. The maximum charge stored in the capacitor would be higher if S3 had remained open.
Answer: D. UUUUUUmmm???