11. Which of the following graphs represents the tension in the cable as a function of displacement angle as a pendulum swings through a complete cycle?
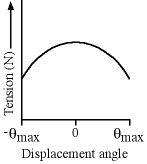
Is apparently the answer, and I sort of understand the explanation. "The tension in the cable varies with the angle of the cable with respect to the surface to which the cable is attached. When the pendulum bob points straight down, the tension must offset the entire weight as well as counterbalance the centripetal force, because there is no net force on the pendulum bob. However, when the bob is at its highest point (and motionless), the tension is reduced, because there is no centripetal force to offset. Only the cosine portion of the weight must be offset, since there is a net force on the pendulum bob. This means that the tension magnitude constantly oscillates between a maximum and minimum. This eliminates choices A and B. Because tension is maximum when the cable points straight down, the graph must show a maximum tension when the displacement angle, θ, is equal to zero. The best answer is D."
But why is there no centipetal force at the top ( or an angle) of a pendulum?

Is apparently the answer, and I sort of understand the explanation. "The tension in the cable varies with the angle of the cable with respect to the surface to which the cable is attached. When the pendulum bob points straight down, the tension must offset the entire weight as well as counterbalance the centripetal force, because there is no net force on the pendulum bob. However, when the bob is at its highest point (and motionless), the tension is reduced, because there is no centripetal force to offset. Only the cosine portion of the weight must be offset, since there is a net force on the pendulum bob. This means that the tension magnitude constantly oscillates between a maximum and minimum. This eliminates choices A and B. Because tension is maximum when the cable points straight down, the graph must show a maximum tension when the displacement angle, θ, is equal to zero. The best answer is D."
But why is there no centipetal force at the top ( or an angle) of a pendulum?
