4
411309
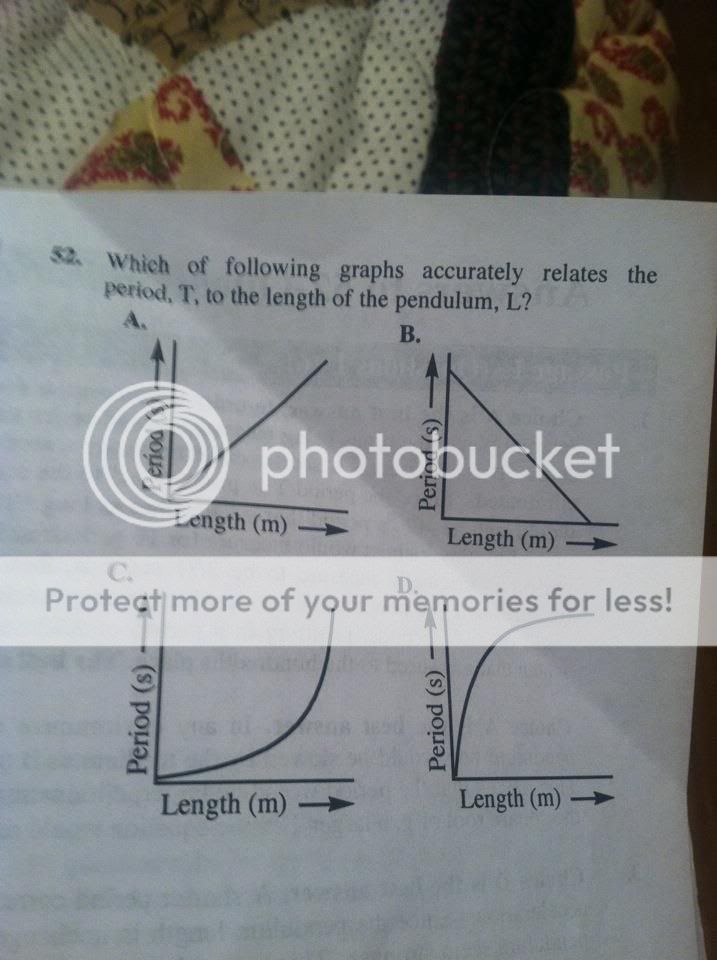
TBR says it's D but I said C. The answer explanation says it bends toward the axis with greatest change and says the X axis is the greatest change. Correct me if im wrong, but isnt it bending towards the x axis in C?


TBR says it's D but I said C. The answer explanation says it bends toward the axis with greatest change and says the X axis is the greatest change. Correct me if im wrong, but isnt it bending towards the x axis in C?
according to the formula T^2 is proportional to L so as T increases a little bit L will increase alot. When looking at graphs that has direct proportionality the graph curves toward the item that increases alot. In this case it is L . So the answer is D and it is curving toward the X-axis which is L
TBR says it's D but I said C. The answer explanation says it bends toward the axis with greatest change and says the X axis is the greatest change. Correct me if im wrong, but isnt it bending towards the x axis in C?
Nm, I get it I just had to look at it again. D corresponds to exponential change in length. I just have trouble applying their "curve to" method it confuses mean by what they mean by that exactly.
Yea that method/shortcut is probably the only thing in TBR that I have not incorporated into my strategy. It doesn't make sense to me either.
I can pick out the best answer, but looking at this again I'm not completely sure why the graph flattens out as L increases?
Yea but that graph (the one you linked to) doesn't plateau nearly as quickly as the TBR graph. I know it's the best answer, but it's not entirely accurate is it?
Like I said, I can pick out the best answer, but I wasn't necessarily sure that the shape of the graph in D is completely accurate.
Like I said, I can pick out the best answer, but I wasn't necessarily sure that the shape of the graph in D is completely accurate.


Here's sqrt(x), you can decide for yourself if the resemblance is good enough or not.
And x^2, just for reference.
What software do you use?
Mathematica. You can write a single line and then right click the graphic and save it as an image file. 👍
Handy. And expensive!
